Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T19:32:32.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Osculatory Packings by Spheres

Published online by Cambridge University Press:  20 November 2018

David W. Boyd
David W. Boyd*
Affiliation:
California Institute of Technology, Pasadena, California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If U is an open set in Euclidean N-space EN which has finite Lebesgue measure |U| then a complete packing of U by open spheres is a collection C={Sn} of pairwise disjoint open spheres contained in U and such that Σ∞n=1|Sn| = |U|. Such packings exist by Vitali's theorem. An osculatory packing is one in which the spheres Sn are chosen recursively so that from a certain point on Sn+1 is the largest possible sphere contained in 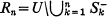(Here S- will denote the closure of a set S). We give here a simple proof of the "well-known" fact that an osculatory packing is a complete packing. Our method of proof shows also that for osculatory packings, the Hausdorff dimension of the residual set 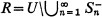is dominated by the exponent of convergence of the radii of the Sn.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 1 , March 1970 , pp. 59 - 64
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Boyd, D. W., Lower bounds for the disk-packing constant, Math. Comp. (to appear).Google Scholar
2. Davis, P. J., Simple quadratures in the complex plane, Pac. J. Math. 15 (1965), 813-824.Google Scholar
3. Gilbert, E. N., Randomly packed and solidly packed spheres, Canad. J. Math. 16 (1964), 286-298.Google Scholar
4. Hirst, K. E., The Apollonian packing of circles, J. Lond. Math. Soc. 42 (1967), 281-291.Google Scholar
5. Kasner, E., and Supnick, F., The Appollonian packing of circles, Proc. Nat. Acad. Sci. U.S.A. 29 (1943), 378-384.Google Scholar
6. Larman, D. G., On the exponent of convergence of a packing of spheres, Mathematika 13 (1966), 57-59.Google Scholar
7. Larman, D. G., On the Besicovitch dimension of the residual set of arbitrarily packed disks in the plane, J. Lond. Math. Soc. 42 (1967), 292-302.Google Scholar
8. Larman, D. G., A note on the Besicovitch dimension of the closest packing of spheres in Rn, Proc. Comb. Phil. Soc. 62 (1966), 193-195.Google Scholar
9. Melzak, Z. A., Infinite packings of disks, Canad. J. Math. 18 (1966), 838-852.Google Scholar
10., On the solid-packing constant for circles, Math. Comp. 23 (1969), 169-172.Google Scholar
11. Mergelyan, S. N., Uniform approximation to functions of a complex variable, Uspehi Mat. Nauk 7 (1952), 31-122; Amer. Math. Soc. Trans. 101 (1954), 21.Google Scholar
12. Wesler, O., An infinite packing theorem for spheres, Proc. Amer. Math. Soc. 11 (1960), 324-326.Google Scholar
13. Wilker, J. B., Open disk packings of a disk, Canad. Math. Bull. 10 (1967), 395-415.Google Scholar