Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T19:14:37.405Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal Control Strategies for Virus Spreading in Inhomogeneous Epidemic Dynamics

Published online by Cambridge University Press:  20 November 2018

Yilun Shang
Yilun Shang*
Affiliation:
Institute for Cyber Security, University of Texas at San Antonio, San Antonio, Texas 78249, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study the spread of virus/worm in computer networks with a view to addressing cyber security problems. Epidemic models have been applied extensively to model the propagation of computer viruses, which characterize the fact that infected machines may spread malware to other hosts connected to the network. 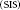In our framework, the dynamics of hosts evolves according to a modified inhomogeneous Susceptible-Infectious-Susceptible $\left( \text{SIS} \right)$ epidemic model with time-varying transmission rate and recovery rate. The infection of computers is subject to direct attack as well as propagation among hosts. Based on optimal control theory, optimal attack strategies are provided by minimizing the cost (equivalently maximizing the profit) of the attacker. We present a threshold function of the fraction of infectious hosts, which captures the dynamically evolving strategies of the attacker and reflects the persistence of virus spreading. Moreover, our results indicate that if the infectivity of a computer worm is low and the computers are installed with antivirus software with high reliability, the intensity of attacks incurred will likely be low. This agrees with our intuition.

Keywords

49J1592D30computer virusepidemic dynamicsoptimal controlnetwork security
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 3 , 01 September 2013 , pp. 621 - 629
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Bailey, M., Cooke, E., Jahanian, F., Xu, Y. and Karir, M., A survey of botnet technology and defenses. In: Proc. Cybersecurity Applications & Technology Conference For Homeland Security (CATCH ‘09), Washington, DC, March 2009, 299–304.Google Scholar
[2] Ball, F., D, Mollison and G, Scalia-Tomba, Epidemics with two levels of mixing. Ann. Appl. Prob. 7 (1997, 46–89. http://dx.doi.org/10.1214/aoap/1034625252 Google Scholar
[3] Ball, F., D. Sirl and Trapman, P., Analysis of a stochastic SIR epidemic on a random network incorporating household structure. Math. Biosci. 224 (2010, 53–73. http://dx.doi.org/10.1016/j.mbs.2009.12.003 Google Scholar
[4] Bensoussan, A., Kantarcioglu, M. and Hoe, C., A game-theoretical approach for finding optimal strategies in a botnet defense model. In: Proc. GameSec ‘10, Berlin, Germany, 2010, 135–148.Google Scholar
[5] Berger, N., Borgs, C., Chayes, J. T. and Saberi, A., On the spread of viruses on the internet. In: Proc. 16th Annual ACM-SIAM Symposium on Discrete Algorithms, ACM, New York, 2005, 301–310.Google Scholar
[6] Bertsekas, D. P., Dynamic Programming and Optimal Control. Vol. 1. Third edition. Athena Scientific, Belmont, MA, 2005.Google Scholar
[7] Britton, T., Stochastic epidemic models: a survey. Math. Biosci. 225 (2010, 24–35. http://dx.doi.org/10.1016/j.mbs.2010.01.006 Google Scholar
[8] Britton, T., Kypraios, T. and O'Neill, P. D., Inference for epidemics with three levels of mixing: methodology and application to a measles outbreak. Scand. J. Stat. 38 (2011, 578–599.Google Scholar
[9] Cohen, F., Computer viruses: theory and experiments. Computer and Security 6 (1987, 22–35.Google Scholar
[10] Diekmann, O. and Heesterbeek, J. A. P. , Mathematical Epidemiology of Infectious Disease. JohnWiley & Sons, Chichester, 2000.Google Scholar
[11] Fultz, N. and Grossklags, J., Blue versus red: towards a model of distributed security attacks. Lecture Notes in Computer Science 5628 (2009, 167–183.Google Scholar
[12] Higgins, K. J., Conficker botnet ‘dead in the water’, researcher says. Technical Report, http://www. darkreading.com/vulnerability management/security/attacks/showArticle.jhtml?articleID=224201115.Google Scholar
[13] Lelarge, M., Economics of malware: epidemic risks model, network externalities and incentives. In: Proc. 47th Annual Allerton Conference on Communication, Control, and Computing, IEEE Press, Piscataway, NJ, 2009, 1353–1360.Google Scholar
[14] Li, Z., Liao, Q. and Striegel, A., Botnet economics: uncertainty matters. In: Managing Information Risk and the Economics of Security, Springer, New York, 2009, 245–267.Google Scholar
[15] Piqueira, J. R. C. and Araujo, V. O., A modified epidemiological model for computer viruses. Appl. Math. Comput. 213 (2009, 355–360. http://dx.doi.org/10.1016/j.amc.2009.03.023 Google Scholar
[16] Provos, N. and Holz, T., Virtual Honeypots—From Botnet Tracking to Intrusion Detection. Pearson Education Inc., Boston, 2008.Google Scholar
[17] Shang, Y., Optimal attack strategies in a dynamic botnet defense model. Appl. Math. Inf. Sci. 6 (2012, 29–33.Google Scholar
[18] Shang, Y., Likelihood estimation for stochastic epidemics with heterogeneous mixing populations. Int. J. Comput. Math. Sci. 6 (2012, 34–38.Google Scholar
[19] Shang, Y., Multi-agent coordination in directed moving neighborhood random networks. Chinese Phys. B 19 (2010, 070201.Google Scholar
[20] van den Broek, J. and Heesterbeek, J. A. P., Nonhomogeneous birth and death models for epidemic outbreak data. Biostatistics 8 (2007, 453–467.Google Scholar
[21] van den Broek, J. and Nishiura, H., Using epidemic prevalence data to jointly estimate reproduction and removal. Ann. Appl. Stat. 3 (2009, 1505–1520. http://dx.doi.org/10.1214/09-AOAS270 Google Scholar
[22] Yeung, D. and Petrosyan, L., Cooperative Stochastic Differential Games. Springer, New York, 2006.Google Scholar
[23] Zou, C., Duffield, N., D. Towsley andGong, W., Adaptive defense against various network attacks. IEEE Journal on Selected Areas in Communications 24 (2006, 1877–1888.Google Scholar