Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T16:59:58.263Z Has data issue: false hasContentIssue false
  • English
  • Français

Operators on Anti-dual pairs: Self-adjoint Extensions and the Strong Parrott Theorem

Part of: Topological linear spaces and related structures Topological (rings and) algebras with an involution General theory of linear operators

Published online by Cambridge University Press:  24 January 2020

Zsigmond Tarcsay  and
Tamás Titkos
Zsigmond Tarcsay
Affiliation:
Department of Applied Analysis and Computational Mathematics, Eötvös Loránd University, Pázmány Péter sétány 1/c., Budapest H-1117, Hungary Email: [email protected]
Tamás Titkos
Affiliation:
Alfréd Rényi Institute of Mathematics, Reáltanoda utca 13-15., Budapest H-1053, Hungary BBS University of Applied Sciences, Alkotmány u. 9., Budapest H-1054, Hungary Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The aim of this paper is to develop an approach to obtain self-adjoint extensions of symmetric operators acting on anti-dual pairs. The main advantage of such a result is that it can be applied for structures not carrying a Hilbert space structure or a normable topology. In fact, we will show how hermitian extensions of linear functionals of involutive algebras can be governed by means of their induced operators. As an operator theoretic application, we provide a direct generalization of Parrott’s theorem on contractive completion of 2 by 2 block operator-valued matrices. To exhibit the applicability in noncommutative integration, we characterize hermitian extendibility of symmetric functionals defined on a left ideal of a 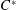$C^{\ast }$-algebra.

Keywords

Self-adjoint operatorsymmetric operatoranti-dualityself-adjoint extensionParrott theorem*-algebrapositive functionalhermitian functional

MSC classification

Primary: 47A20: Dilations, extensions, compressions
Secondary: 46A22: Theorems of Hahn-Banach type; extension and lifting of functionals and operators 46A20: Duality theory 46K10: Representations of topological algebras with involution
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 4 , December 2020 , pp. 813 - 824
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Canadian Mathematical Society 2020

Footnotes

The corresponding author Zs. Tarcsay was supported by DAAD-TEMPUS Cooperation Project “Harmonic Analysis and Extremal Problems” (grant no. 308015). Project no. ED 18-1-2019-0030 (Application-specific highly reliable IT solutions) has been implemented with the support provided from the National Research, Development and Innovation Fund of Hungary, financed under the Thematic Excellence Programme funding scheme.

T. Titkos was supported by the Hungarian National Research, Development and Innovation Office - NKFIH (Grant No. PD128374 and Grant No. K115383), by the János Bolyai Research Scholarship of the Hungarian Academy of Sciences, and by the ÚNKP-18-4-BGE-3 New National Excellence Program of the Ministry of Human Capacities.

References

Ando, T. and Hara, T., Another approach to the strong Parrott theorem. J. Math. Anal. Appl. 171(1992), 125–130. https://doi.org/10.1016/0022-247X(92)90380-VCrossRefGoogle Scholar
Ando, T. and Nishio, K., Positive self-adjoint extensions of positive symmetric operators. Tohoku Math. J. 22(1970), 65–75. https://doi.org/10.2748/tmj/1178242861CrossRefGoogle Scholar
Baidiuk, D. and Hassi, S., Completion, extension, factorization, and lifting of operators. Math. Ann. 364(2016), 1415–1450. https://doi.org/10.1007/s00208-015-1261-5CrossRefGoogle Scholar
Bakonyi, M. and Woerdeman, H. J., On the strong Parrott completion problem. Proc. Amer. Math. Soc. 117(1993), 429–433. https://doi.org/10.2307/2159179CrossRefGoogle Scholar
Blackadar, B., Operator algebras: theory of C ∗-algebras and von Neumann algebras. Encyclopaedia of Mathematical Sciences, 122, Operator Algebras and Non-Commutative Geometry III, Springer-Verlag, Berlin, 2006. https://doi.org/10.1007/3-540-28517-2CrossRefGoogle Scholar
Coddington, E. A. and de Snoo, H. S. V., Positive selfadjoint extensions of positive symmetric subspaces. Math. Zeitschriften 159(1978), 203–214. https://doi.org/10.1007/BF01214571CrossRefGoogle Scholar
Foias, C. and Tannenbaum, A., A strong Parrott theorem. Proc. Amer. Math. Soc. 106(1989), 777–784. https://doi.org/10.2307/2047435CrossRefGoogle Scholar
Hassi, S., Malamud, M. M., and de Snoo, H.S.V., On Krein’s extension theory of nonnegative operators. Math. Nachr. 274/275(2004), 40–73. https://doi.org/10.1002/mana.200310202CrossRefGoogle Scholar
Kadison, R. and Ringrose, J., Fundamentals of the theory of operator algebras. Vol. I. Elementary theory. Pure and Applied Mathematics, 100, Academic Press, New York, 1983.Google Scholar
Krein, M. G., The theory of self-adjoint extensions of semi-bounded Hermitian transformations and its applications. I. Rec. Math. [Mat. Sbornik] N.S. 20(1947), no. 62, 431–495.Google Scholar
Malamud, M. M., On some classes of extensions of sectorial operators and dual pairs of contractions. In: Recent advances in operator theory. Operator theory: advances and applications, 124, Birkhäuser, Basel, 2001, pp. 401–449.CrossRefGoogle Scholar
Parrott, S., On the quotient norm and the Sz.-Nagy–Foias lifting theorem. J. Functional Analysis 30(1978), 311–328. https://doi.org/10.1016/0022-1236(78)90060-5CrossRefGoogle Scholar
Paulsen, V. and Raghupathi, M., An introduction to the theory of reproducing kernel Hilbert spaces. Cambridge Studies in Advanced Mathematics, 152, Cambridge University Press, Cambridge, 2016. https://doi.org/10.1017/CBO9781316219232CrossRefGoogle Scholar
Schwartz, L., Sous-espaces hilbertiens d’espaces vectoriels topologiques et noyaux associés (noyaux reproduisants). J. Analyse Math. 13(1964), 115–256. https://doi.org/10.1007/BF02786620CrossRefGoogle Scholar
Sebestyén, Z., On representability of linear functionals on *-algebras. Period. Math. Hungar. 15(1984), 233–239. https://doi.org/10.1007/BF02454172CrossRefGoogle Scholar
Sebestyén, Z., Operator extensions on Hilbert space. Acta Sci. Math. (Szeged) 57(1993), 233–248.Google Scholar
Sebestyén, Z., Szűcs, Zs., and Tarcsay, Zs., Extensions of positive operators and functionals. Linear Algebra Appl. 472(2015), 54–80. https://doi.org/10.1016/j.laa.2015.01.028CrossRefGoogle Scholar
Sebestyén, Z., Tarcsay, Zs., and Titkos, T., A characterization of positive normal functionals on the full operator algebra. In: The diversity and beauty of applied operator theory. Oper. Theory Adv. Appl., 268, Birkhäuser, Cham, 2018, pp. 443–447.CrossRefGoogle Scholar
Tarcsay, Zs. and Titkos, T., Operators on anti-dual pairs: Generalized Krein–von Neumann extension. 2018. arxiv:1810.02619Google Scholar
Timotin, D., A note on Parrott’s strong theorem. J. Math. Anal. Appl. 171(1992), 288–293. https://doi.org/10.1016/0022-247X(92)90390-YCrossRefGoogle Scholar
Yamada, A., Parrott’s theorem and bounded solutions of a system of operator equations. Complex Anal. Oper. Theory 11(2017), 961–976. https://doi.org/10.1007/s11785-016-0559-yCrossRefGoogle Scholar