Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T05:28:57.685Z Has data issue: false hasContentIssue false
  • English
  • Français

Operator valued analogues of multidimensional Bohr’s inequality

Part of: Spaces and algebras of analytic functions General theory of linear operators Holomorphic functions of several complex variables

Published online by Cambridge University Press:  10 January 2022

Vasudevarao Allu Open the ORCID record for Vasudevarao Allu [Opens in a new window]  and
Himadri Halder
Vasudevarao Allu*
Affiliation:
School of Basic Sciences, Indian Institute of Technology Bhubaneswar, Bhubaneswar 752050, Odisha, India e-mail: [email protected]
Himadri Halder
Affiliation:
School of Basic Sciences, Indian Institute of Technology Bhubaneswar, Bhubaneswar 752050, Odisha, India e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

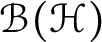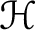Let $\mathcal {B}(\mathcal {H})$ be the algebra of all bounded linear operators on a complex Hilbert space $\mathcal {H}$ . In this paper, we first establish several sharp improved and refined versions of the Bohr’s inequality for the functions in the class 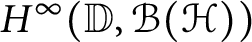$H^{\infty }(\mathbb {D},\mathcal {B}(\mathcal {H}))$ of bounded analytic functions from the unit disk 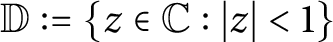$\mathbb {D}:=\{z \in \mathbb {C}:|z|<1\}$ into 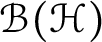$\mathcal {B}(\mathcal {H})$ . For the complete circular domain 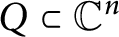$Q \subset \mathbb {C}^{n}$ , we prove the multidimensional analogues of the operator valued Bohr-type inequality which can be viewed as a special case of the result by G. Popescu [Adv. Math. 347 (2019), 1002–1053] for free holomorphic functions on polyballs. Finally, we establish the multidimensional analogues of several improved Bohr’s inequalities for operator valued functions in Q.

Keywords

Bohr radiuscomplete circular domainhomogeneous polynomialoperator valued analytic functions

MSC classification

Primary: 32A05: Power series, series of functions 32A10: Holomorphic functions 47A56: Functions whose values are linear operators (operator and matrix valued functions, etc., including analytic and meromorphic ones)
Secondary: 47A63: Operator inequalities 30H05: Bounded analytic functions
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 4 , December 2022 , pp. 1020 - 1035
Check for updates
Copyright
© Canadian Mathematical Society, 2022

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahamed, M. B., Allu, V., and Halder, H., The Bohr Phenomenon for analytic functions on shifted disks. Ann. Fenn. Math. 47(2022), 103–120.CrossRefGoogle Scholar
Aizenberg, L., Multidimensional analogues of Bohr’s theorem on power series. Proc. Amer. Math. Soc. 128(2000), 1147–1155.CrossRefGoogle Scholar
Aizenberg, L., Aytuna, A., and Djakov, P., Generalization of theorem on Bohr for bases in spaces of holomorphic functions of several complex variables. J. Math. Anal. Appl. 258(2001), 429–447.CrossRefGoogle Scholar
Aizenberg, L., Generalization of results about the Bohr radius for power series. Stud. Math. 180(2007), 161–168.CrossRefGoogle Scholar
Alkhaleefah, S. A., Kayumov, I. R., and Ponnusamy, S., On the Bohr inequality with a fixed zero coefficient. Proc. Amer. Math. Soc. 147(2019), 5263–5274.CrossRefGoogle Scholar
Allu, V. and Halder, H., Bohr operator on operator valued polyanalytic functions on simply connected domains, https://arxiv.org/pdf/2111.10883.pdf.Google Scholar
Anderson, J. M. and Rovnyak, J., On generalized Schwarz-Pick estimates. Mathematika 53(2006), 161–168.CrossRefGoogle Scholar
Aytuna, A. and Djakov, P., Bohr property of bases in the space of entire functions and its generalizations. Bull. Lond. Math. Soc. 45(2013), no. 2, 411–420.CrossRefGoogle Scholar
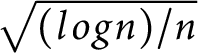Bayart, F., Pellegrino, D., and Seoane-Sep Úlveda, J. B., The Bohr radius of the $n$ -dimensional polydisk is equivalent to $\sqrt{(logn)/ n}$ . Adv. Math. 264(2014), 726–746.CrossRefGoogle Scholar
Bénéteau, C., Dahlner, A., and Khavinson, D., Remarks on the Bohr phenomenon. Comput. Methods Funct. Theory 4(2004), no. 1, 1–19.CrossRefGoogle Scholar
Bhowmik, B. and Das, N., Bohr phenomenon for operator-valued functions. Proc. Edinburgh Math. Soc. 64((2021)), no. 1, 72–86.CrossRefGoogle Scholar
Blasco, O., The Bohr radius of a Banach space , In Vector measures, integration and related topics, 5964, Oper. Theory Adv. Appl., 201, Birkhäuser Verlag, Basel, 2010.Google Scholar
Boas, H. P. and Khavinson, D., Bohr’s power series theorem in several variables. Proc. Amer. Math. Soc. 125(1997), 2975–2979.CrossRefGoogle Scholar
Bohr, H., A theorem concerning power series. Proc. Lond. Math. Soc. s2-13(1914), 1–5.CrossRefGoogle Scholar
Bombieri, E., Sopra un teorema di H. Bohr e G. Ricci sulle funzioni maggioranti delle serie di potenze. Boll. Un. Mat. Ital. 17(1962), 276–282.Google Scholar
Defant, A. and Frerick, L., A logarithmic lower bound for multi-dimenional bohr radii. Israel J. Math. 152(2006), 17–28.CrossRefGoogle Scholar
Defant, A., Frerick, L., Ortega-Cerd À, J., Ounaïes, M., and Seip, K., The Bohnenblust-Hille inequality for homogeneous polynomils in hypercontractive. Ann. of Math. 174(2011), 512–517.CrossRefGoogle Scholar
Dixon, P. G., Banach algebras satisfying the non-unital von Neumann inequality. Bull. Lond. Math. Soc. 27(1995), no. 4, 359–362.CrossRefGoogle Scholar
Djakov, P. B. and Ramanujan, M. S., A remark on Bohr’s theorem and its generalizations. J. Anal. 8(2000), 65–77.Google Scholar
Evdoridis, S., Ponnusamy, S., and Rasila, A., Improved Bohr’s inequality for shifted disks. Results Math. 76(2021), 14.CrossRefGoogle Scholar
Garcia, S. R., Mashreghi, J., and Ross, W. T., Finite Blaschke products and their connections, Springer, Cham, 2018.10.1007/978-3-319-78247-8CrossRefGoogle Scholar
Liu, M. S. and Ponnusamy, S., Multidimensional analogues of refined Bohr’s inequality. Proc. Amer. Math. Soc. 149(2021), 2133–2146.CrossRefGoogle Scholar
Paulsen, V. I., Gelu Popescu and Dinesh Singh, on Bohr’s inequality. Proc. Lond. Math. Soc. s3-85(2002), 493–512.CrossRefGoogle Scholar
Paulsen, V. I. and Singh, D., Bohr’s inequality for uniform algebras. Proc. Amer. Math. Soc. 132(2004), 3577–3579.CrossRefGoogle Scholar
Popescu, G., Bohr inequalities for free holomorphic functions on polyballs. Adv. Math. 347(2019), 1002–1053.CrossRefGoogle Scholar