Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T13:01:43.764Z Has data issue: false hasContentIssue false
  • English
  • Français

One-Dimensional Representations of the Cycle Subalgebra of a Semi-Simple Lie Algebra

Published online by Cambridge University Press:  20 November 2018

F. W. Lemire
F. W. Lemire*
Affiliation:
University of British Columbia, Vancouver, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let L denote a semi-simple, finite dimensional Lie algebra over an algebraically closed field K of characteristic zero. If denotes a Cartan subalgebra of L and 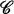denotes the centralizer of in the universal enveloping algebra U of L, then it has been shown that each algebra homomorphism 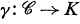(called a "mass-function" on 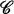) uniquely determines a linear irreducible representation of L. The technique involved in this construction is analogous to the Harish-Chandra construction [2] of dominated irreducible representations of L starting from a linear functional 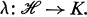. The difference between the two results lies in the fact that all linear functionals on are readily obtained, whereas since 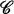is in general a noncommutative algebra the construction of mass-functions is decidedly nontrivial.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 4 , December 1970 , pp. 463 - 467
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Bouwer, I. Z., Standard representations of simple Lie algebras, Canad. J. Math. 20 (1968), 344-361.Google Scholar
2. Harish-Chandra, , On some applications of the universal enveloping algebra of a semi-simple Lie algebra, Trans. Amer. Math. Soc. 70 (1951), 28-99.Google Scholar
3. Lemire, F. W., Irreducible representations of a simple Lie algebra admitting a one-dimensional weight space, Proc. Amer. Math. Soc. 19 (1968), 1161-1164.Google Scholar
4. Jacobson, N., Lie algebras, Interscience, New York, 1962.Google Scholar
5. de Siebenthal, J., Sur certains modules dans une algèbre de Lie semi-simple, Comment. Math. Helv. 44(1969), 1-44.Google Scholar