Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T13:12:57.223Z Has data issue: false hasContentIssue false
  • English
  • Français

On Y. C. Wong's Conjecture

Published online by Cambridge University Press:  20 November 2018

D. K. Datta
D. K. Datta*
Affiliation:
University of Rhode Island, Kingston, Rhode Island
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M be an n-dimensional connected C∞ manifold with a linear connection Γ. M is said to be of recurrent curvature with respect to Γ if the corresponding curvature tensor R satisfies [1], [4]

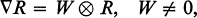
where Δ denotes covariant derivative with respect to Γ and W is a nonzero covector called the recurrence co-vector. Let T be the torsion of Γ.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 4 , December 1970 , pp. 423 - 424
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Nomizu, K. and Kobayashi, S., Foundations of differential geometry, Interscience 1963.Google Scholar
2. Takano, K., On Y.C. Wong's conjecture, Tensor 15 (1964), 175-180.Google Scholar
3. Wong, Y. C. and Yano, K., Projectively flat spaces with recurrent curvature, Comment. Math. Helv. 35 (1961), 223-232.Google Scholar
4. Wong, Y. C., Recurrent tensors on a linearly connected differentiable manifold, Trans. Amer. Math. Soc. 99 (1961), 325-341.Google Scholar
5. Wong, Y. C., Linear connections with zero torsion and recurrent curvature, Trans. Amer. Math. Soc. 102 (1962), 471-506.Google Scholar
6. Yamaguchi, S., On infinitesimal projective transformations in non-Riemannian recurrent space, Tensor 18 (1967), 271-278.Google Scholar
7. Yano, K., Theory of lie derivatives, Interscience, 1957.Google Scholar