It is known that any non-archimedean Fréchet space of countable type is isomorphic to a subspace of 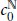$c_{0}^{\mathbb{N}}$. In this paper we prove that there exists a non-archimedean Fréchet space 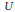$U$ with a basis 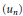$({{u}_{n}})$ such that any basis 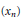$({{x}_{n}})$ in a non-archimedean Fréchet space 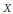$X$ is equivalent to a subbasis 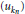$({{u}_{kn}})$ of 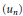$({{u}_{n}})$. Then any non-archimedean Fréchet space with a basis is isomorphic to a complemented subspace of 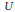$U$. In contrast to this, we show that a non-archimedean Fréchet space 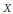$X$ with a basis 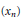$({{x}_{n}})$ is isomorphic to a complemented subspace of 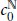$c_{0}^{\mathbb{N}}$ if and only if 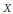$X$ is isomorphic to one of the following spaces: 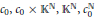${{c}_{0}},\,{{c}_{0}}\,\times \,{{\mathbb{K}}^{\mathbb{N}}},\,{{\mathbb{K}}^{\mathbb{N}}},\,c_{0}^{\mathbb{N}}$. Finally, we prove that there is no nuclear non-archimedean Fréchet space $H$ with a basis 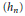$({{h}_{n}})$ such that any basis 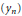$({{y}_{n}})$ in a nuclear non-archimedean Fréchet space 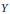$Y$ is equivalent to a subbasis 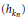$({{h}_{kn}})$ of 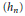$({{h}_{n}})$.