No CrossRef data available.
Published online by Cambridge University Press: 18 November 2021
We prove several results on unavoidable families of meromorphic functions. For instance, we give new examples of families of cardinality 3 that are unavoidable with respect to the set of meromorphic functions on
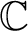 $\mathbb C$
. We further obtain families consisting of less than three functions that are unavoidable with respect to certain subsets of meromorphic functions. In the other direction, we show that for every meromorphic function f, there exists an entire function that avoids f on
$\mathbb C$
. We further obtain families consisting of less than three functions that are unavoidable with respect to certain subsets of meromorphic functions. In the other direction, we show that for every meromorphic function f, there exists an entire function that avoids f on
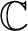 $\mathbb C$
.
$\mathbb C$
.