Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T09:31:02.150Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Square of the First Zero of the Bessel Function Jv(z)

Published online by Cambridge University Press:  20 November 2018

Árpád Elbert  and
Panayiotis D. Siafarikas
Árpád Elbert
Affiliation:
Mathematical Institute of the Hungarian Academy of Science Budapest POB. 428 1376 Hungary
Panayiotis D. Siafarikas
Affiliation:
Department of Mathematics University of Patras Patras Greece
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

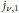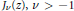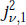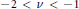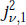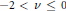Let ${{j}_{v,1}}$ be the smallest (first) positive zero of the Bessel function ${{J}_{v}}(z),\,v\,>\,-\,1$, which becomes zero when $v$ approaches −1. Then $j_{v,1}^{2}$ can be continued analytically to $-2\,<\,v\,<\,-1$, where it takes on negative values. We show that $j_{v,1}^{2}$ is a convex function of $v$ in the interval $-2\,<\,v\,\le \,0$, as an addition to an old result [Á. Elbert and A. Laforgia, SIAM J. Math. Anal. 15(1984), 206–212], stating this convexity for 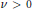$v\,>\,0$. Also the monotonicity properties of the functions 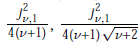$\frac{j_{v,1}^{2}}{4(v+1)},\,\frac{j_{v,1}^{2}}{4(v+1)\sqrt{v+2}}$ are determined. Our approach is based on the series expansion of Bessel function 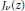${{J}_{v}}(z)$ and it turned out to be effective, especially when 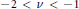$-2\,<\,v\,<\,-1$.

Keywords

33A40
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 1 , 01 March 1999 , pp. 56 - 67
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Putterman, S. J., M. Kac and Uhlenbeck, G. E., Possible origin of the quantized vortices in He, II. Phys. Rev. Lett. 29 (1972), 546–549.Google Scholar
[2] Elbert, Á. and Laforgia, A., On the square of the zeros of Bessel functions. SIAM J. Math. Anal. 15 (1984), 206–212.Google Scholar
[3] Hurwitz, A., Ueber die Nullstellen der Bessel’schen Function. Math. Ann. 33 (1889), 246–266.Google Scholar
[4] Ifantis, E. K. and Siafarikas, P. D., A differential inequality for the positive zeros of Bessel functions. J. Comp. Appl. Math. 44 (1992), 115–120.Google Scholar
[5] Ismail, M. E. H. and Muldoon, M. E., On the variation with respect to a parameter of zeros of Bessel and q-Bessel functions. J. Math. Anal. Appl. 135 (1988), 187–207.Google Scholar
[6] Ismail, M. E. H. and Muldoon, M. E., Bounds for the small real and purely imaginary zeros of Bessel and related functions. Methods Appl. Anal. (1) 2 (1995), 1–21.Google Scholar
[7] Kokologiannaki, C. G., Muldoon, M. E. and Siafarikas, P. D., A unimodal property of purely imaginary zeros of Bessel and related functions. Canad. Math. Bull. 37 (1994), 365–373.Google Scholar
[8] Lewis, J. T. and Muldoon, M. E., Monotonicity and convexity property of zeros of Bessel functions. SIAM J. Math. Anal. 8 (1977), 171–178.Google Scholar
[9] Piessens, R., A series expansion for the first positive zero of Bessel function. Math. Comp. 42 (1984), 195–197.Google Scholar
[10] Watson, G. N., A treatise on the theory of Bessel Functions. 2nd edn, Cambridge University Press, 1944.Google Scholar