Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T16:32:38.795Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Representation of Mappings of Tychonov Spaces as Restrictions of Linear Transformations

Published online by Cambridge University Press:  20 November 2018

Kim-Peu Chew  and
Kok-Keong Tan
Kim-Peu Chew
Affiliation:
Dalhousie University, Halifax, Nova Scotia, Canada
Kok-Keong Tan
Affiliation:
Dalhousie University, Halifax, Nova Scotia, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (X, τ) be a Tychonov space and 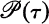the collection of all families of pseudometrics on X generating the topology τ on X. Let f:X→X and c>0. Then f is said to be a topological c-homothety if there exists some B in 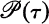such that d(f(x), f(y))=cd(x, y) for all d ∈ B and all x, y in X (see [4]). We say that f can be linearized in L as a c-homothety if there exists a linear topological space L, and a topological embedding i:X→L such that i(f(x))=ci(x) for all x in X (see [4]).f is said to be squeezing if 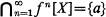for some a in X.

Keywords

54.3554.654.85Topological c-homothetyLinear representations of selfmaps
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 19 , Issue 1 , 01 March 1976 , pp. 53 - 57
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. Edelstein, M., On the representation of mappings of compact metrizable spaces as restrictions of linear transformations, Can. J. Math. Vol. XXII (1970) 372–375.Google Scholar
2. Edelstein, M. and Swaminathan, S., On the representation of mappings of normal Hausdorff spaces as restrictions of linear transformations, Roma Accademia Nazionale Del Lindel. Serie VIII, Vol. L (1971) 676–678.Google Scholar
3. Gillman, L. and Jerison, M., Rings of continuous functions, Van Nostrand, Princeton, N.J. (1960).Google Scholar
4. Janos, L., Topological homothetics on compact Hausdorff spaces, Proc. Amer. Math. Soc. Vol. 21 (1969) 562–568.Google Scholar