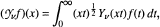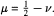Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rooney, P. G.
1995.
On the representation of functions by the Hankel and some related transformations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 125,
Issue. 3,
p.
449.
Tuan, Vum Kim
1996.
On the range of the Y-transform.
Bulletin of the Australian Mathematical Society,
Vol. 54,
Issue. 2,
p.
329.
A.Kilbas, Anatoly
and
Trujillo, Juan J.
2000.
Generalized hankel transform no space.
Integral Transforms and Special Functions,
Vol. 9,
Issue. 4,
p.
271.
Gromak, Elena V.
and
Kilbas, Anatoly A.
2005.
Asymptotic expansions of 𝒴ηtransform.
Integral Transforms and Special Functions,
Vol. 16,
Issue. 5-6,
p.
407.
Sitnik, S. M.
Skoromnik, O. V.
and
Shlapakov, S. A.
2022.
Multi-Dimensional Generalized Integral Transform in the Weighted Spaces of Summable Functions.
Lobachevskii Journal of Mathematics,
Vol. 43,
Issue. 6,
p.
1408.
Sitnik, S. M.
Skoromnik, O. V.
and
Papkopvich, M. V.
2023.
Differential Equations, Mathematical Modeling and Computational Algorithms.
Vol. 423,
Issue. ,
p.
193.
SITNIK, S.
SKOROMNIK, O.
and
PAPKOVICH, M.
2023.
TWO-DIMENSIONAL INTEGRAL H-TRANSFORM
IN WEIGHTED SPACES OF SUMMABLE FUNCTIONS.
HERALD OF POLOTSK STATE UNIVERSITY. Series С FUNDAMENTAL SCIENCES,
p.
93.


 transformation, defined by
transformation, defined by