Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T01:29:19.389Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Radius of Comparison of a Commutative C*-algebra

Published online by Cambridge University Press:  20 November 2018

George A. Elliott  and
Zhuang Niu
George A. Elliott
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario M5S 2E4 e-mail: [email protected]
Zhuang Niu
Affiliation:
Department of Mathematics, University of Wyoming, Laramie, Wyoming, USA 82071 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 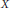$X$ be a compact metric space. A lower bound for the radius of comparison of the 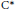${{\text{C}}^{*}}$-algebra 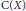$\text{C}\left( X \right)$ is given in terms of 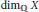${{\dim}_{\mathbb{Q}}}\,X$, where 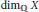${{\dim}_{\mathbb{Q}}}\,X$ is the cohomological dimension with rational coefficients. If 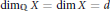${{\dim}_{\mathbb{Q}}}\,X\,=\,\dim\,X\,=\,d$, then the radius of comparison of the 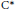${{\text{C}}^{*}}$-algebra 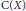$C\left( X \right)$ is 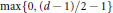$\max \left\{ 0,\,\left( d\,-\,1 \right)/\,2\,-\,1 \right\}$ if $d$ is odd, and must be either 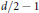${d}/{2}\;\,-\,1$ or 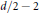${d}/{2}\;\,-\,2$ if $d$ is even (the possibility 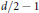${d}/{2}\;\,-\,1$ does occur, but we do not know if the possibility 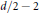${d}/{2}\;\,-\,2$ can also occur).

Keywords

46L80Cuntz semigroupcomparison radiuscohomology dimensioncovering dimension
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 4 , 01 December 2013 , pp. 737 - 744
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Blackadar, B., Robert, L., Tikuisis, A. P., Toms, A. S., and Winter, W., An algebraic approach to the radius of comparison. Trans. Amer. Math. Soc. 364 (2012), no. 7, 3657–3674.Google Scholar
[2] Coward, K. T., Elliott, G. A., and Ivanescu, C., The Cuntz semigroup as an invariant for C*-algebras. J. Reine Angew. Math. 623 (2008), 161–193. http://dx.doi.org/10.1515/CRELLE.2008.075 Google Scholar
[3] Dranishnikov, A. N., Cohomological dimension theory of compact metric spaces. Topology Atlas Invited Contribution. 6 (2001), 61 pp. arxiv:math/0501523Google Scholar
[4] Dydak, J. and Walsh, J. J., Infinite-dimensional compacta having cohomological dimension two: an application of the Sullivan conjecture. Topology 32 (1993), no. 1, 93–104. http://dx.doi.org/10.1016/0040-9383(93)90040-3 Google Scholar
[5] Elliott, G. A., Robert, L., and Santiago, L., The cone of lower semicontinuous traces on a C*-algebra. Amer. J. Mat. 133 (2011), no. 4, 969–1005. http://dx.doi.org/10.1353/ajm.2011.0027 Google Scholar
[6] Hatcher, A., Algebraic topology, Cambridge University Press, Cambridge, 2002.Google Scholar
[7] Husemoller, D., Fibre bundles. Third ed., Graduate Texts in Mathematics, 20, Springer-Verlag, New York, 1994.Google Scholar
[8] Karoubi, M., K-Theory. An introduction, Grundlehren der MathematischenWissenschaften, 226, Springer-Verlag, Berlin-New York, 1978.Google Scholar
[9] Kodama, Y., Note on an absolute neighborhood extensor for metric spaces. J. Math. Soc. Japa. 8 (1956), 206–215. http://dx.doi.org/10.2969/jmsj/00830206 Google Scholar
[10] Nagami, K., Dimension theory. Pure and Applied Mathematics, 37, Academic Press, New York-London, 1970.Google Scholar
[11] Toms, A. S., Flat dimension growth for C*-algebras. J. Funct. Anal. 238 (2006), no. 2, 678–708. http://dx.doi.org/10.1016/j.jfa.2006.01.010 Google Scholar
[12] Toms, A. S., Stability in the Cunz semigroup of a commutative C*-algebra. Proc. Lond. Math. Soc. 96 (2008), no. 1, 1–25. http://dx.doi.org/10.1112/plms/pdm023 Google Scholar
[13] Toms, A. S., Comparison theory and smooth minimal C*-dynamics. Comm. Math. Phys. 289 (2009), no. 2, 401–433. http://dx.doi.org/10.1007/s00220-008-0665-4 Google Scholar
[14] Walsh, J. J., Dimension, cohomological dimension, and cell-like mappings. In: Shape theory and geometric topology (Dubrovnik, 1981), Lecture Notes in Mathematics, 870, Springer, Berlin-New York, 1981.Google Scholar