Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T16:04:33.984Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Number of Divisors of the Quadratic Form m2 + n2

Published online by Cambridge University Press:  20 November 2018

Gang Yu
Gang Yu*
Affiliation:
Department of Mathematics The University of Georgia Athens, Georgia 30602 U.S.A., e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For an integer 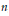$n$, let 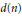$d\left( n \right)$ denote the ordinary divisor function. This paper studies the asymptotic behavior of the sum

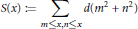$$S\left( x \right)\,:=\sum\limits_{m\le x,n\le x}{d\left( {{m}^{2}}+{{n}^{2}} \right)}$$
.

It is proved in the paper that, as 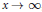$x\,\to \,\infty $,

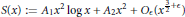$$S(x):={{A}_{1}}{{x}^{2}}\log x+{{A}_{2}}{{x}^{2}}+{{O}_{\in }}({{x}^{\frac{3}{2}+\in }}),$$

where 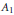${{A}_{1}}$ and 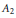${{A}_{2}}$ are certain constants and 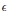$\in $ is any fixed positive real number.

The result corrects a false formula given in a paper of Gafurov concerning the same problem, and improves the error 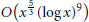$O({{x}^{\frac{5}{3}}}\,{{(\log \,x)}^{9}})$ claimed by Gafurov.

Keywords

11G0514H52Divisorlarge sieveexponential sums
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 2 , 01 June 2000 , pp. 239 - 256
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Davenport, H., Multiplicative Number Theory. Graduate Texts in Math. 74, Revised by L, H.. Montgomery Springer, 1980.Google Scholar
[2] Friedlander, J. B. and Iwaniec, H., The polynomial x2 + y4 captures its primes. preprint.Google Scholar
[3] Fouvry, E. and Iwaniec, H., Gaussian primes. Acta Arith. 129(1997), 249–287.Google Scholar
[4] Gafurov, N.,On the number of divisors of a quadratic form. Proc. Steklov Inst.Math. (1993), 137–148.Google Scholar
[5] Hooley, C., On the number of divisors of quadratic polynomials. ActaMath. 110(1963), 97–114.Google Scholar
[6] Iwaniec, H. and Mozzochi, C. J., On the divisor and circle problems. J.Number Theory 29(1988), 60–93.Google Scholar
[7] Vaaler, J. D., Some extremal problems in Fourier analysis. Bull. Amer.Math. Soc. (2) 12(1985), 183–216.Google Scholar