No CrossRef data available.
Article contents
On the Notion of Visibility of Torsors
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let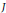 
$J$ be an abelian variety and 
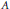$A$ be an abelian subvariety of 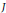$J$ , both defined over 
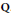$Q$. Let 
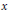$x$ be an element of 
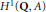${{H}^{1}}\left( Q,\,A \right)$. Then there are at least two definitions of 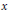$x$ being visible in 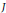$J$: one asks that the torsor corresponding to 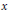$x$ be isomorphic over 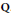$Q$ to a subvariety of 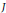$J$, and the other asks that 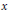$x$ be in the kernel of the natural map 
$
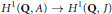{{H}^{1}}\left( Q,\,A \right)\,\to \,{{H}^{1}}\left( \text{Q},\,J \right)$. In this article, we clarify the relation between the two definitions.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013
References
[1]
Agashe, A., On invisible elements of the Tate-Shafarevich group.
C. R. Acad. Sci. Paris Sér. I Math.
328(1999), no. 5, 369–374.
Google Scholar
[2]
Agashe, A., A visible factor of the Heegner index. Math. Res. Lett.
17(2010), no. 6, 1065–1077.
Google Scholar
[3]
Agashe, A., Visibility and the Birch and Swinnerton-Dyer conjecture for analytic rank zero.
arxiv:0908.3823.Google Scholar
[4]
Agashe, A., Visibility and the Birch and Swinnerton-Dyer conjecture for analytic rank one.
Int. Math. Res. Not. (IMRN)
15(2009), 2899–2913.
Google Scholar
[5]
Agashe, A., A visible factor of the special L-value.
J. Reine Angew. Math.
644(2010), 159–187.
http://dx.doi.org/10.1515/CRELLE.2010.055
Google Scholar
[6]
Agashe, A., Ribet, K., and Stein, W. A., The modular degree, congruence primes, and multiplicity one. To appear in a special Springer volume in honor of Serge Lang, http://www.math.fsu.edu/_agashe/moddeg3.html
Google Scholar
[7]
Agashe, A. and Stein, W., Visible evidence for the Birch and Swinnerton-Dyer conjecture for modular abelian varieties of analytic rank zero.
Math. Comp.
74(2005), no. 249, 455–484.
http://dx.doi.org/10.1090/S0025-5718-04-01644-8
Google Scholar
[8]
Cremona, J. E. and Mazur, B., Visualizing elements in the Shafarevich-Tate group.
Experiment. Math.
9(2000), no. 1, 13–28.
Google Scholar
[9]
Mazur, B., Three lectures about the arithmetic of elliptic curves. Handout at the ArizonaWinter School, http://swc.math.arizona.edu/notes/NotesAll.html.
Google Scholar
[10]
Milne, J. S., Etale cohomology.
Princeton Mathematical Series, 33, Princeton University Press,Google Scholar
You have
Access