Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T11:16:36.502Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Norm of the Beurling–Ahlfors Operator in Several Dimensions

Published online by Cambridge University Press:  20 November 2018

Tuomas P. Hytönen
Tuomas P. Hytönen*
Affiliation:
Department of Mathematics and Statistics, University of Helsinki, FI-00014 Helsinki, Finlande-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The generalized Beurling–Ahlfors operator $S$ on 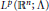${{L}^{p}}({{\mathbb{R}}^{n}};\,\Lambda )$, where 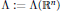$\Lambda \,:=\,\Lambda ({{\mathbb{R}}^{n}})$ is the exterior algebra with its natural Hilbert space norm, satisfies the estimate

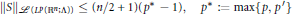$$||S||L\left( {{L}^{p}}\left( {{\mathbb{R}}^{n}};\Lambda \right) \right)\le \left( n/2+1 \right)\left( {{p}^{*}}-1 \right),\,\,\,{{p}^{*}}:=\,\max \{p,\,{{p}^{'}}\}.$$
.

This improves on earlier results in all dimensions 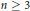$n\,\ge \,3$. The proof is based on the heat extension and relies at the bottom on Burkholder's sharp inequality for martingale transforms.

Keywords

42B2060G46
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 1 , 01 March 2011 , pp. 113 - 125
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Bañuelos, R. and Méndez-Hernández, P. J., Space-time Brownian motion and the Beurling-Ahlfors transform. Indiana Univ. Math. J. 52(2003), no. 4, 981–990.Google Scholar
[2] Bañuelos, R. and Janakiraman, P., Lp-bounds for the Beurling-Ahlfors transform. Trans. Amer. Math. Soc. 360(2008), no 7, 3603–3612. doi:10.1090/S0002-9947-08-04537-6Google Scholar
[3] Bañuelos, R. and Lindeman, A. II, A martingale study of the Beurling-Ahlfors transform in R n . J. Funct. Anal. 145(1997), no. 1, 224–265. doi:10.1006/jfan.1996.3022Google Scholar
[4] Bañuelos, R. and Wang, G., Sharp inequalities for martingales with applications to the Beurling-Ahlfors and Riesz transforms. Duke Math. J. 80(1995), no. 3, 575–600. doi:10.1215/S0012-7094-95-08020-XGoogle Scholar
[5] Burkholder, D. L., Boundary value problems and sharp inequalities for martingale transforms. Ann. Probab. 12(1984), no. 3, 647–702. doi:10.1214/aop/1176993220Google Scholar
[6] Dragičević, O. and Volberg, A., Bellman function, Littlewood-Paley estimates and asymptotics for the Ahlfors-Beurling operator in Lp (ℂ) . Indiana Univ. Math. J. 54(2005), no. 4, 971–995. doi:10.1512/iumj.2005.54.2554Google Scholar
[7] Dragičević, O. and Volberg, A., Bellman functions and dimensionless estimates of Littlewood-Paley type. J. Operator Theory 56(2006), no. 1, 167–198.Google Scholar
[8] Geiss, S., Montgomery-Smith, S., and Saksman, E., On singular integral and martingale transforms. Trans. Amer. Math. Soc. 362(2010), no. 2, 553–575. doi:10.1090/S0002-9947-09-04953-8Google Scholar
[9] Guerre-Delabrière, S., Some remarks on complex powers of (–Δ) and UMD spaces. Illinois J. Math. 35(1991), no. 3, 401–407.Google Scholar
[10] Hytönen, T., Aspects of probabilistic Littlewood-Paley theory in Banach spaces. In: Banach spaces and their applications in analysis, Walter de Gruyter, Berlin, 2007, pp. 343–355.Google Scholar
[11] Iwaniec, T. and Martin, G., Quasiregular mappings in even dimensions. Acta Math. 170(1993), no. 1, 29–81. doi:10.1007/BF02392454Google Scholar
[12] Lehto, O., Remarks on the integrability of the derivatives of quasiconformal mappings. Ann. Acad. Sci. Fenn. Ser. A I 371(1965), 8 pp.Google Scholar
[13] Petermichl, S., Slavin, L., and Wick, B. D., New estimates for the Beurling-Ahlfors operator on differential forms. J. Operator Theory, to appear.Google Scholar
[14] Voloberg, A. and Nazarov, F., Heat extension of the Beurling operator and estimates for its norm. (Russian) Algebra i Analiz 15(2003), no. 4, 142–158; translation in St. Petersburg Math. J. 15(2004), no. 4, 563–573.Google Scholar