Hostname: page-component-55f67697df-sqlfs Total loading time: 0 Render date: 2025-05-12T15:25:03.464Z Has data issue: false hasContentIssue false
  • English
  • Français

On the metric dimension of circulant graphs

Part of: Graph theory

Published online by Cambridge University Press:  28 September 2023

Rui Gao ,
Yingqing Xiao  and
Zhanqi Zhang
Rui Gao
Affiliation:
School of Statistics and Mathematics, Shandong University of Finance and Economics, Jinan, Shandong 250014, China e-mail: [email protected]
Yingqing Xiao
Affiliation:
School of Mathematics, Hunan University, Changsha, Hunan 410082, China e-mail: [email protected]
Zhanqi Zhang*
Affiliation:
School of Mathematics and Computational Science, Hunan University of Science and Technology, Xiangtan, Hunan 411201, China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this note, we bound the metric dimension of the circulant graphs 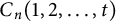$C_n(1,2,\ldots ,t)$. We shall prove that if 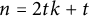$n=2tk+t$ and if t is odd, then 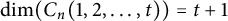$\dim (C_n(1,2,\ldots ,t))=t+1$, which confirms Conjecture 4.1.1 in Chau and Gosselin (2017, Opuscula Mathematica 37, 509–534). In Vetrík (2017, Canadian Mathematical Bulletin 60, 206–216; 2020, Discussiones Mathematicae. Graph Theory 40, 67–76), the author has shown that 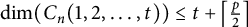$\dim (C_n(1,2,\ldots ,t))\leq t+\left \lceil \frac {p}{2}\right \rceil $ for 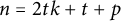$n=2tk+t+p$, where 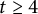$t\geq 4$ is even, 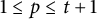$1\leq p\leq t+1$, and 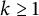$k\geq 1$. Inspired by his work, we show that 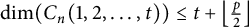$\dim (C_n(1,2,\ldots ,t))\leq t+\left \lfloor \frac {p}{2}\right \rfloor $ for 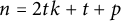$n=2tk+t+p$, where 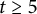$t\geq 5$ is odd, 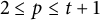$2\leq p\leq t+1$, and 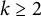$k\geq 2$.

Keywords

Metric dimensionresolving setcirculant graphdistance

MSC classification

Primary: 05C35: Extremal problems 05C12: Distance in graphs
Type
Article
Information
Canadian Mathematical Bulletin , Volume 67 , Issue 2 , June 2024 , pp. 328 - 337
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was supported by the Natural Science Foundation of Shandong Province (Grant No. ZR2021QG036).

References

Borchert, A. and Gosselin, S., The metric dimension of circulant graphs and Cayley hypergraphs . Util. Math. 106(2018), 125–147.Google Scholar
Chau, K. and Gosselin, S., The metric dimension of circulant graphs and their Cartesian products . Opuscula Math. 37(2017), 509–534. https://doi.org/10.7494/OpMath.2017.37.4.509CrossRefGoogle Scholar
Grigorious, C., Kalinowski, T., Ryan, J., and Stephen, S., The metric dimension of the circulant graph $C(n,\pm \left\{1,2,3,4\right\})$ . Australas. J. Combin. 69(2017), 417–441.Google Scholar
Grigorious, C., Manuel, P., Miller, M., Rajan, B., and Stephen, S., On the metric dimension of circulant graphs and Harary graphs . Appl. Math. Comput. 248(2014), 47–54. https://doi.org/10.1016/j.amc.2014.09.045 Google Scholar
Harary, F. and Melter, R. A., On the metric dimension of a graph . Ars Combin. 2(1976), 191–195.Google Scholar
Johnson, M., Structure-activity maps for visualizing the graph variables arising in drug design . J. Biopharm. Stat. 3(1993), no. 2, 203–236. https://doi.org/10.1080/10543409308835060 CrossRefGoogle ScholarPubMed
Johnson, M., Browsable structure-activity datasets . In: Carbó-Dorca, R. and Mezey, P. (eds.), Advances in molecular similarity, JAI Press Inc., Stamford, CT, 1998, pp. 153–170. https://doi.org/10.1016/s1873-9776(98)80014-x Google Scholar
Khuller, S., Raghavachari, B., and Rosenfeld, A., Landmarks in graphs . Discret. Appl. Math. 70(1996), 217–229. https://doi.org/10.1016/0166-218x(95)00106-2 CrossRefGoogle Scholar
Slater, P. J., Leaves of trees . Congr. Numer. 14(1975), 549–559.Google Scholar
Vetrík, T., The metric dimension of circulant graphs . Can. Math. Bull. 60(2017), 206–216. https://doi.org/10.4153/cmb-2016-048-1 CrossRefGoogle Scholar
Vetrík, T., On the metric dimension of circulant graphs with $4$ generators . Contrib. Discrete Math. 12(2017), 104–114. https://doi.org/10.11575/cdm.v12i2.62479 Google Scholar
Vetrík, T., On the metric dimension of directed and undirected circulant graphs . Discuss. Math. Graph Theory. 40(2020), 67–76. https://doi.org/10.7151/dmgt.2110CrossRefGoogle Scholar