Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T05:25:50.100Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Metric Compactification of Infinite-dimensional $\ell _{p}$ Spaces

Part of: Fairly general properties Global differential geometry Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  28 December 2018

Armando W. Gutiérrez
Armando W. Gutiérrez*
Affiliation:
Department of Mathematics and Systems Analysis, Aalto University, Otakaari 1 Espoo, Finland Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

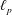The notion of metric compactification was introduced by Gromov and later rediscovered by Rieffel. It has been mainly studied on proper geodesic metric spaces. We present here a generalization of the metric compactification that can be applied to infinite-dimensional Banach spaces. Thereafter we give a complete description of the metric compactification of infinite-dimensional 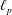$\ell _{p}$ spaces for all 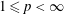$1\leqslant p<\infty$. We also give a full characterization of the metric compactification of infinite-dimensional Hilbert spaces.

Keywords

metric compactificationhorofunction compactificationmetric functionalBanach space

MSC classification

Primary: 54D35: Extensions of spaces (compactifications, supercompactifications, completions, etc.)
Secondary: 53C23: Global geometric and topological methods (à la Gromov); differential geometric analysis on metric spaces 46B45: Banach sequence spaces
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 3 , September 2019 , pp. 491 - 507
Copyright
© Canadian Mathematical Society 2018 

Footnotes

This work was supported by the Academy of Finland, Grant No. 288318.

References

Ballmann, W., Lectures on spaces of nonpositive curvature , DMV Seminar, 25, Birkhäuser Verlag, Basel, 1995. https://doi.org/10.1007/978-3-0348-9240-7.Google Scholar
Ballmann, W., Gromov, M., and Schroeder, V., Manifolds of nonpositive curvature , Progress in Mathematics, 61, Birkhäuser Boston, Inc., Boston, MA, 1985. https://doi.org/10.1007/978-1-4684-9159-3.Google Scholar
Bridson, M. R. and Haefliger, A., Metric spaces of non-positive curvature , Grundlehren der Mathematischen Wissenschaften, 319, Springer-Verlag, Berlin, 1999. https://doi.org/10.1007/978-3-662-12494-9.Google Scholar
Clarkson, J. A., Uniformly convex spaces . Trans. Amer. Math. Soc. 40(1936), 396–414. https://doi.org/10.2307/1989630.Google Scholar
Friedland, S. and Freitas, P. J., p-metrics on GL(n, ℂ)/Un and their Busemann compactifications . Linear Algebra Appl. 376(2004), 1–18. https://doi.org/10.1016/S0024-3795(03)00661-X.Google Scholar
Gaubert, S. and Vigeral, G., A maximin characterisation of the escape rate of non-expansive mappings in metrically convex spaces . Math. Proc. Cambridge Philos. Soc. 152(2012), 341–363. https://doi.org/10.1017/S0305004111000673.Google Scholar
Gouëzel, S. and Karlsson, A., Subadditive and multiplicative ergodic theorems. 2015. arxiv:1509.07733.Google Scholar
Gromov, M., Hyperbolic manifolds, groups and actions . In: Riemann surfaces and related topics: Proceedings of the 1978 Stony Brook Conference (State Univ. New York, Stony Brook, N.Y., 1978) , Ann. of Math. Stud., 97, Princeton University Press, Princeton, NJ, 1981, pp. 183–213.Google Scholar
Gutiérrez, A. W., The horofunction boundary of finite-dimensional ℓ p spaces . Colloq. Math. 155(2019), 51–65. https://doi.org/10.4064/cm7320-3-2018.Google Scholar
Ji, L. and Schilling, A.-S., Polyhedral horofunction compactification as polyhedral ball. 2016. arxiv:1607.00564.Google Scholar
Karlsson, A., Metz, V., and Noskov, G. A., Horoballs in simplices and Minkowski spaces . Int. J. Math. Math. Sci. pages Art. 2006, 23656. https://doi.org/10.1155/IJMMS/2006/23656.Google Scholar
Karlsson, A., Dynamics of Hilbert nonexpansive maps . In: Handbook of Hilbert geometry , IRMA Lect. Math. Theor. Phys., 22, Eur. Math. Soc., Zürich, 2014, pp. 263–273.Google Scholar
Karlsson, A. and Ledrappier, F., Noncommutative ergodic theorems . In: Geometry, rigidity, and group actions , Chicago Lectures in Math., Univ. Chicago Press, Chicago, IL, 2011, pp. 396–418.Google Scholar
Kelley, J. L., General topology. Reprint of the 1955 edition [Van Nostrand, Toronto, Ont.], Graduate Texts in Mathematics, 27, Springer-Verlag, New York-Berlin, 1975.Google Scholar
Khamsi, M. A. and Kirk, W. A., An introduction to metric spaces and fixed point theory , Pure and Applied Mathematics (New York), Wiley-Interscience, New York, 2001. https://doi.org/10.1002/9781118033074.Google Scholar
Maher, J. and Tiozzo, G., Random walks on weakly hyperbolic groups . J. Reine Angew. Math. 742(2018), 187–239. https://doi.org/10.1515/crelle-2015-0076.Google Scholar
Rieffel, M. A., Group C ∗-algebras as compact quantum metric spaces . Doc. Math. 7(2007), 605–651.Google Scholar
Walsh, C., The horofunction boundary of finite-dimensional normed spaces . Math. Proc. Cambridge Philos. Soc. 142(2007), 497–507. https://doi.org/10.1017/S0305004107000096.Google Scholar
Walsh, C., Hilbert and Thompson geometries isometric to infinite-dimensional Banach spaces. 2016. arxiv:1610.07508.Google Scholar