Hostname: page-component-7bb8b95d7b-495rp Total loading time: 0 Render date: 2024-09-13T17:12:57.417Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Inversion of General Transformations*

Published online by Cambridge University Press:  20 November 2018

P. G. Rooney
P. G. Rooney*
Affiliation:
University of Toronto
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let k be the kernel of a “general transformation”; that is, k(x) / x ϵ L2 (0,∞), and if x and y are positive

1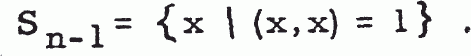

Then it is well known (see for example [8; Theorems 129 and 131]) that if the transform of fϵL2 (0,∞) is g, that is, if

2

then the inverse transform is given by

3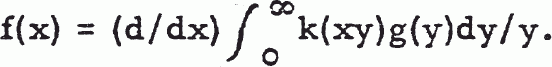

In practice, the inversion formula (3) is often hard to use. For example, the integral may be too difficult to evaluate; moreover, since (2) requires a differentiation, it is not well suited for numerical calculation. Hence it seems worthwhile to find other methods for inverting the transformation.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 2 , Issue 1 , 01 January 1959 , pp. 19 - 24
Copyright
Copyright © Canadian Mathematical Society 1959

Footnotes

*

This paper was written while the author was a fellow at the 1958 Summer Research Institute of the Canadian Mathematical Congress, Kingston, Ontario.

References

1. Boas, R.P. and Widder, D.V., An inversion formula for the Laplace integral, Duke Math, J. 6(1940), 1-26.Google Scholar
2. Doetsch, G., Handbuch der Laplace Transformation, (Basel, 1950).Google Scholar
3. Erdélyi, A. et al., Tables of Integral Transforms, v.1, (New York, 1954).Google Scholar
4. Hirschman, I.I., A new representation and inversion theory for the Laplace integral, Duke Math. J. 15(1948), 473-494.Google Scholar
5. Rooney, P.G., A new inversion and representation theory for the Laplace transformation, Can. J. Math. 4(1952), 436-444.Google Scholar
6. Rooney, P.G., On an inversion formula for the Laplace transformation, Can. J. Math. 7(1955), 101-115.Google Scholar
7. Rooney, P.G., On the representation of functions as Fourier transforms, Can. J, Math. - to appear,Google Scholar
8. Titchmarsh, E.C., Introduction to the Theory of Fourier Integrals, 2nd ed., (Oxford, 1948).Google Scholar
9. Widder, D.V., The Laplace Transform, (Princeton, 1941).Google Scholar