Hostname: page-component-7bb8b95d7b-fmk2r Total loading time: 0 Render date: 2024-09-06T17:39:55.221Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Injective and Projective Limit of Complexes

Published online by Cambridge University Press:  20 November 2018

Krishna Tewari
Krishna Tewari*
Affiliation:
Banaras Hindu University, Varanasi U-P, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a commutative ring with unit. Let (Aα, φ βα) (α ≤ β) (resp. (Bα, ψαβ) (α ≤ β)) be an infective (resp. projective) system of R-algebras indexed by a directed set I; let ((Xα, dα), fβα) (α ≤ β) (resp. ((Yα, δα), gαβ) (α≤β)) be an injective (resp. projective) system of complexes, indexed by the same set I, such that for each αϵI, (Xα, dα) (resp. (Yα, δα)) is a complex over Aα (resp. over Bα). The purpose of this paper is to show that the covariant functor 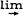from the category of all such injective systems of complexes and complex homomorphisms over the R-algebra 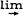Aα is such that it associates with an injective system ((Uα, dα), hβα) of universal complexes a universal complex over 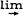Aα whereas the same is not true of the covariant functor 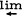the category of all such projective systems of complexes and their maps.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 8 , Issue 3 , April 1965 , pp. 291 - 305
Copyright
Copyright © Canadian Mathematical Society 1965

Footnotes

*

The author wishes to express her thanks to Professor B. Banaschewski for his guidance during the preparation of this work.

References

1. Berger, R., Űber Verschiedene Differentenbegriffe. Sitzungsberichte der Heidelberger Akademie der Wissenschaften Mathematischnaturwissenschaftliche Klasse, 196.Google Scholar
2. Bourbaki, N., Algèbre Commutative, Chapter II, (Hermann and Cie, Paris).Google Scholar
3. Bourbaki, N., Algèbre, Chapter V, (Hermann and Cie, Paris).Google Scholar
4. Bourbaki, N., Theory of Sets, Chapter IV, (Hermann and Cie, Paris).Google Scholar
5. Chevalley, C., Fundamental Concepts of Algebra, Academic Press Inc., N. Y. Google Scholar
6. Kähler, E., Algebra und Differentialrechnung. Bericht űber die Mathematiker Tagung in Berlin, Vol. 14, Bis. 18, January 1953.Google Scholar
7. Zariski, O. and Samuel, P., Commutative Algebra, Vol. II. University Series In Higher Mathematics.Google Scholar