Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T06:08:54.140Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Inequality for Volume and Minkowskian Thickness

Published online by Cambridge University Press:  20 November 2018

Gennadiy Averkov
Gennadiy Averkov*
Affiliation:
Fakultät für Mathematik, Technische Universität Chemnitz, D-09107 Chemnitz, Deutschland e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a centrally symmetric convex body $B$ in 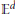${{\mathbb{E}}^{d}}$, we denote by 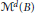${{\mathcal{M}}^{d}}\left( B \right)$ the Minkowski space (i.e., finite dimensional Banach space) with unit ball $B$. Let 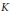$K$ be an arbitrary convex body in 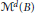${{\mathcal{M}}^{d}}\left( B \right)$. The relationship between volume 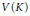$V\left( K \right)$ and the Minkowskian thickness (= minimal width) 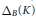${{\Delta }_{B}}\left( K \right)$ of 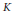$K$ can naturally be given by the sharp geometric inequality 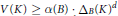$V\left( K \right)\ge \alpha \left( B \right)\cdot {{\Delta }_{B}}{{\left( K \right)}^{d}}$, where 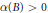$\alpha \left( B \right)>0$. As a simple corollary of the Rogers-Shephard inequality we obtain that 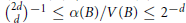${{\left( _{d}^{2d} \right)}^{-1}}\le \alpha \left( B \right)/V\left( B \right)\le {{2}^{-d}}$ with equality on the left attained if and only if $B$ is the difference body of a simplex and on the right if $B$ is a cross-polytope. The main result of this paper is that for 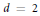$d=2$ the equality on the right implies that $B$ is a parallelogram. The obtained results yield the sharp upper bound for the modified Banach–Mazur distance to the regular hexagon.

Keywords

52A4046B20Convex bodygeometric inequalitythicknessMinkowski spaceBanach spacenormed spacereduced bodyBanach-Mazur compactum(modified) Banach-Mazur distancevolume ratio
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 2 , 01 June 2006 , pp. 185 - 195
Copyright
Copyright © Canadian Mathematical Society 2006

References

[Asp60] Asplund, E., Comparision between plane symmetric convex bodies and parallelograms. Math. Scand. 8(1960), 171–180.Google Scholar
[Ave] Averkov, G., A monotonicity lemma for bodies of constant Minkowskian width, J. Geom., to appear.Google Scholar
[Ave03a] Averkov, G., Constant Minkowskian width in terms of double normals. J. Geom. 77(2003), no. 1-2, 1–7.Google Scholar
[Ave03b] Averkov, G., On cross-section measures in Minkowski spaces. Extracta Math. 18(2003), no. 2, 201–208.Google Scholar
[Ave03c] Averkov, G., On the geometry of simplices in Minkowski spaces. Stud. Univ. Žilina Math. Ser. 16(2003), no. 1, 1–14.Google Scholar
[Ave05] Averkov, G., On planar convex bodies of given Minkowskian thickness and least possible area. Arch. Math. (Basel) 84 2005), no. 2, 183–192.Google Scholar
[AvM04] Averkov, G. and Martini, H., A characterization of constant width in Minkowski planes. Aequationes Math. 68(2004), 38–45.Google Scholar
[BF74] Bonnesen, T. and Fenchel, W., Theorie der konvexen Körper. Springer-Verlag, Berlin, 1974, Berichtigter Reprint.Google Scholar
[Cha66] Chakerian, G. D., Sets of constant width. Pacific J. Math. 19(1966), 13–21.Google Scholar
[CG85] Chakerian, G. D. and Ghandehari, M. A., The Fermat problem in Minkowski spaces. Geom. Dedicata 17(1985), no. 3, 227–238.Google Scholar
[Grü63] Grünbaum, B., Measures of symmetry for convex sets. Proc. Sympos. Pure Math. 7(1963), pp. 233–270.Google Scholar
[Hei78] Heil, E., Kleinste konvexe Körper gegebener Dicke. Preprint No. 453, Fachbereich Mathematik der TH Darmstadt, 1978.Google Scholar
[Khr01a] Khrabrov, A. I., Distances between spaces with unconditional bases. Function theory and mathematical analysis. J. Math. Sci. (New York) 107(2001), no. 3, 3952–3962,Google Scholar
[Khr01b] Khrabrov, A. I., Generalized volume ratios and the Banach-Mazur distance., transl. Math. Notes 70(2001), no. 5-6, 838–846.Google Scholar
[Las90] Lassak, M., Reduced convex bodies in the plane. Israel J. Math. 70(1990), no. 3, 365–379.Google Scholar
[LasM] Lassak, M. and Martini, H., Reduced bodies in Minkowski space. Acta Math. Hungar. 106(2005), no. 1-2, 17–26.Google Scholar
[Lev52] Levi, F. W., Über zwei Sätze von Herrn Besicovitch. Arch. Math. 3(1952), 125–129.Google Scholar
[LM93] Lindenstrauss, J. and Milman, V. D., The local theory of normed spaces and its applications to convexity. In: Handbook of Convex Geometry, Vol. A, B, North-Holland, Amsterdam, 1993, pp. 1149–1220.Google Scholar
[Mac51] Macbeath, A. M., A compactness theorem for affine equivalence-classes of convex regions. Canad. J. Math. 3(1951), 54–61.Google Scholar
[Mah39] Mahler, K., Ein Übertragungsprinzip für konvexe Körper. Časopis Pěst. Mat. Fys. 68(1939), 93–102.Google Scholar
[Mar89] Martini, H., Das Volumen spezieller konvexer Polytope. Elem. Math. 44(1989), no. 5, 113–115.Google Scholar
[MarS] Martini, H. and Swanepoel, K. J., Antinorms and radon curves. submitted.Google Scholar
[McM82] McMullen, P., The volume of certain convex sets. Math. Proc. Cambridge Philos. Soc. 91(1982), no. 1, 91–97.Google Scholar
[MS86] Milman, V. D. and Schechtman, G., Asymptotic theory of finite-dimensional normed spaces. With an appendix by Gromov, M.. Lecture Notes in Mathematics 1200, Springer-Verlag, Berlin, 1986.Google Scholar
[MS03] Martini, H. and Swanepoel, K. J., The geometry of Minkowski spaces—a survey. II. Expo. Math. 22(2004), no. 2, 93–144.Google Scholar
[MSW01] Martini, H., Swanepoel, K. J., and Weiß, G., The geometry of Minkowski spaces—a survey. I. Expo. Math. 19(2001), no. 2, 97–142.Google Scholar
[Pis89] Pisier, G., The volume of convex bodies and Banach space geometry. Cambridge Tracts in Mathematics 94, Cambridge University Press, Cambridge, 1989.Google Scholar
[Rei86] Reisner, S., Zonoids with minimal volume-product. Math. Z. 192(1986), no. 3, 339–346.Google Scholar
[Sch93] Schneider, R., Convex Bodies: The Brunn-Minkowski Theory. Encyclopedia of Mathematics and its Applications, 44, Cambridge University Press, Cambridge, 1993.Google Scholar
[Str81] Stromquist, W., The maximum distance between two-dimensional Banach spaces. Math. Scand. 48(1981), no. 2, 205–225.Google Scholar
[Sza91] Szarek, S. J., On the geometry of the Banach-Mazur compactum. In: Functional Analysis. Lecture Notes in Math. 1470, Springer, Berlin, 1991, pp. 48–59.Google Scholar
[Tho96] Thompson, A. C., Minkowski Geometry. Encyclopedia of Mathematics and its Applications 63, Cambridge University Press, Cambridge, 1996.Google Scholar
[TJ89] Tomczak-Jaegermann, N., Banach-Mazur distances and finite-dimensional operator ideals. Pitman Monographs and Surveys in Pure and Applied Mathematics 38, Longman Scientific & Technical, Harlow, 1989.Google Scholar
[WW91] Wellmann, M. and Wernicke, B., Flächeninhalte gleichseitiger Dreiecke in einer Banach-Minkowskischen Ebene. Wiss. Z. Pädagog. Hochsch. Erfurt/Mühlhausen Math.-Natur. Reihe 27(1991), no. 1, 21–28.Google Scholar