No CrossRef data available.
Article contents
On the Gras Conjecture for Imaginary Quadratic Fields
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this paper we extend K. Rubin's methods to prove the Gras conjecture for abelian extensions of a given imaginary quadratic field 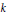 $k$ and prime numbers
$k$ and prime numbers 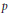 $p$ that divide the number of roots of unity in
$p$ that divide the number of roots of unity in 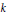 $k$.
$k$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013
References
[1]
Gillard, R., Remarques sur les unités cyclotomiques et les unités elliptiques. J. Number Theory
11 (1979), no. 1, 21–48. http://dx.doi.org/10.1016/0022-314X(79)90018-0
Google Scholar
[2]
Oukhaba, H. and Viguié, S., The Gras conjecture in function fields by Euler systems. Bull. London Math. Soc.
43 (2011), no. 3, 523–535. http://dx.doi.org/10.1112/blms/bdq119
Google Scholar
[3]
Robert, G., Unités de Stark comme unités elliptiques. Prépublication de l’institut Fourier, no. 143, 1989.Google Scholar
[4]
Oukhaba, H. and Viguié, S., Concernant la relation de distribution satisfaite par la fonction ‘ associée à un réseau complexe. Invent. Math. 100 (1990), no. 2, 231–257. http://dx.doi.org/10.1007/BF01231186
Google Scholar
[5]
Oukhaba, H. and Viguié, S., Unités de Stark et racine 12-i`eme canonique. Prépublication de l’institut Fourier, no. 181, 1991.Google Scholar
[6]
Oukhaba, H. and Viguié, S., La racine 12-iéme canoniqueΔ(L)[L: L]/Δ(L). In: Séminaire de Théorie des Nombres, Paris, 1989–90, Progr. Math., 102, Birköuser Boston, Boston, MA, 1992, pp. 209–232.Google Scholar
[7]
Rubin, K., Global units and ideal class groups. Invent. Math. 89 (1987), no. 3, 511–526. http://dx.doi.org/10.1007/BF01388983
Google Scholar
[8]
Rubin, K., The “main conjectures” of Iwasawa theory for imaginary quadratic fields. Invent. Math. 103 (1991), no. 1, 25–68. http://dx.doi.org/10.1007/BF01239508
Google Scholar
[9]
Rubin, K., More “main conjectures” for imaginary quadratic fields. In: Elliptic curves and related topics, CRM Proc. Lecture Notes, 4, American Mathematical Society, Providence, RI, 1994, pp. 23–28.Google Scholar
[10]
Sinnott, W., On the Stickelberger ideal and the circular units of an abelian field. Invent. Math. 62 (1980/81), no. 2, 181–234. http://dx.doi.org/10.1007/BF01389158
Google Scholar
[11]
Stark, H. M., L-functions at s = 1
. IV. First derivatives at s = 0. Adv. in Math. 35 (1980), no. 3, 197–235. http://dx.doi.org/10.1016/0001-8708(80)90049-3
Google Scholar
[12]
Tate, J., Les conjectures de Stark sur les fonctions L d’Artin en s= 0. Lecture notes edited by Dominique Bernardi and Norbert Schappacher, Progress in Mathematics, 47, Birkhäuser Boston, Inc., Boston, MA, 1984.Google Scholar
[13]
Viguié, S., Index-modules and applications. Manuscripta Math. Published online April 6, 2011. http://dx.doi.org/10.1007/s00229-011-0452-y
Google Scholar


