Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T17:10:43.283Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Generalized Hankel and K Transformations

Published online by Cambridge University Press:  20 November 2018

E. L. Koh
E. L. Koh*
Affiliation:
University of Saskatchewan, Regina
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The K transformation (also called the Meijer transformation) has been extended by Zemanian [1; 2] to a class of generalized functions, 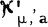For 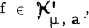, he defined the K transform of f by

(1)

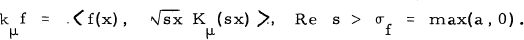
In [2, Section 6.6] the following inversion theorem for the K transform of f is proven:

(2)

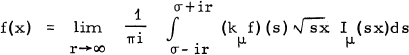
in the sense of weak convergence in D'(I). Here, σ is any fixed real number greater than σf, μ is zero or a complex number with positive real part and D'f(I) is the space of Schwartz distributions on I = (0, ∞).

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 12 , Issue 6 , December 1969 , pp. 733 - 740
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Zemanian, A.H., A distributional K transformation. J. Soc. Ind. Appl. Math. 14 (1966) 1350–1365.Google Scholar
2. Zemanian, A.H., Generalized integral transformations. (Interscience, New York, 1969).Google Scholar
3. Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F.G., Tables of integral transforms, Vol. II. (McGraw-Hill, New York, 1954).Google Scholar
4. Weiss, L., On the foundation of transfer function analysis. Int. J. Eng. Sc. 2 (1964) 343–365.Google Scholar
5. Koh, E. L. and Zemanian, A.H., The complex Hankel and I-transformations of generalized functions. J. Soc. Ind. Appl. Math. 16 (1968) 945–957.Google Scholar
6. Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F.G., Higher transcendental functions, Vol. II. (McGraw-Hill, New York, 1953).Google Scholar