Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T02:59:10.519Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Generalized d’Alembert's and Wilson's Functional Equations on a Compact Group

Published online by Cambridge University Press:  20 November 2018

Belaid Bouikhalene
Belaid Bouikhalene*
Affiliation:
Département de Mathématiques et Informatique, Université Ibn Tofail, Faculté des Sciences, BP 133 Kénitra 14000, Morocco e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 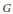$G$ be a compact group.

Let $\sigma$ be a continuous involution of 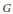$G$. In this paper, we are concerned by the following functional equation

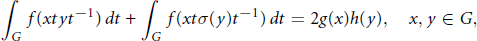$$\int\limits_{G}{f\left( xty{{t}^{-1}} \right)dt}\,+\int\limits_{G}{f\left( xt\sigma \left( y \right){{t}^{-1}} \right)dt}=2g\left( x \right)h\left( y \right),\,\,\,x,y\in G,$$

where 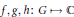$f,g,h:G\mapsto \mathbb{C}$, to be determined, are complex continuous functions on 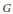$G$ such that 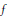$f$ is central. This equation generalizes d’Alembert's and Wilson's functional equations. We show that the solutions are expressed by means of characters of irreducible, continuous and unitary representations of the group 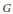$G$.

Keywords

39B3239B4222D1022D1222D15Compact groupsFunctional equationsCentral functionsLie groupsInvariant differential Operators
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 4 , 01 December 2005 , pp. 505 - 522
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Aczèl, J. and Dhombres, J., Functional equations in several variables. Encyclopedia of Mathematics and its Applications 31, Cambridge, Cambridge University Press, 1989.Google Scholar
[2] Bouikhalene, B., On the stability of a class of functional equations. J. Inequal. Pure Appl. Math. 4(2003), Article 104.Google Scholar
[3] Clerc, J. L., Les représentations des groupes compacts. Analyse harmoniques, les Cours du CIMPA, Université de Nancy I, 1980.Google Scholar
[4] Elqorachi, E. and Akkouchi, M., On generalized d’Alembert and Wilson functional equations. Aequationes Math. 66(2003), 241–256.Google Scholar
[5] Helgason, S., Groups and Geometric Analysis. Pure and Applied Mathematics 113, Academic Press, Orlando, FL, 1984.Google Scholar
[6] Hewitt, E. and Ross, K. A., Abstract harmonic analysis. Vol. I and II. Springer-Verlag, Berlin, 1963.Google Scholar
[7] Székelyhidi, L., Almost periodicity and functional equations. Aequationes Math. 26(1983), 163–175.Google Scholar
[8] Weil, A., L’integration dans les groupes topologiques et ses applications. Herman, Paris, 1940.Google Scholar
[9] Weyl, H., Gruppen theorie und Quantenmechanik. 2d ed. Leipzig, 1931.Google Scholar