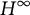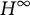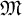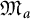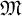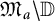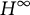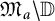1 Formulation of main results
1.1
Recall that for a commutative unital complex Banach algebra A, the maximal ideal space
![]() $\mathfrak M(A)\subset A^\ast $
is the set of nonzero homomorphisms
$\mathfrak M(A)\subset A^\ast $
is the set of nonzero homomorphisms
![]() $A \!\rightarrow \! {\mathbb C}$
endowed with the Gelfand topology, the weak-
$A \!\rightarrow \! {\mathbb C}$
endowed with the Gelfand topology, the weak-
![]() $\ast $
topology of
$\ast $
topology of
![]() $A^\ast $
. It is a compact Hausdorff space contained in the unit sphere of
$A^\ast $
. It is a compact Hausdorff space contained in the unit sphere of
![]() $A^\ast $
. The Gelfand transform defined by
$A^\ast $
. The Gelfand transform defined by
![]() $\hat {a}(\varphi ):=\varphi (a)$
for
$\hat {a}(\varphi ):=\varphi (a)$
for
![]() $a\in A$
and
$a\in A$
and
![]() $\varphi \in \mathfrak M(A)$
is a nonincreasing-norm morphism from A into the Banach algebra
$\varphi \in \mathfrak M(A)$
is a nonincreasing-norm morphism from A into the Banach algebra
![]() $C(\mathfrak M (A))$
of complex-valued continuous functions on
$C(\mathfrak M (A))$
of complex-valued continuous functions on
![]() $\mathfrak M(A)$
.
$\mathfrak M(A)$
.
Let
![]() $H^\infty $
be the Banach algebra of bounded holomorphic functions on the open unit disk
$H^\infty $
be the Banach algebra of bounded holomorphic functions on the open unit disk
![]() $\mathbb {D}\subset {\mathbb C}$
equipped with pointwise multiplication and supremum norm
$\mathbb {D}\subset {\mathbb C}$
equipped with pointwise multiplication and supremum norm
![]() $\lVert \cdot \rVert _\infty $
, and let
$\lVert \cdot \rVert _\infty $
, and let
![]() $\mathfrak M$
be its maximal ideal space. Then the Gelfand transform
$\mathfrak M$
be its maximal ideal space. Then the Gelfand transform
![]() $\hat {\,}: H^\infty \to C(\mathfrak M)$
is an isometry and the map
$\hat {\,}: H^\infty \to C(\mathfrak M)$
is an isometry and the map
![]() $\iota :\mathbb {D}\hookrightarrow \mathfrak M$
taking
$\iota :\mathbb {D}\hookrightarrow \mathfrak M$
taking
![]() $z\in \mathbb {D}$
to the evaluation homomorphism
$z\in \mathbb {D}$
to the evaluation homomorphism
![]() $f\mapsto f(z)$
,
$f\mapsto f(z)$
,
![]() $f\in H^\infty $
, is an embedding with dense image by the celebrated Carleson corona theorem [Reference Carleson5]. In the sequel, we identify
$f\in H^\infty $
, is an embedding with dense image by the celebrated Carleson corona theorem [Reference Carleson5]. In the sequel, we identify
![]() $\mathbb {D}$
with
$\mathbb {D}$
with
![]() $\iota (\mathbb {D})$
.
$\iota (\mathbb {D})$
.
Let
be the pseudohyperbolic metric on
![]() $\mathbb {D}$
.
$\mathbb {D}$
.
For
![]() $m_1,m_2\in \mathfrak M$
, the formula
$m_1,m_2\in \mathfrak M$
, the formula
gives an extension of
![]() $\rho $
to
$\rho $
to
![]() $\mathfrak M\times \mathfrak M$
. The extended function is lower semicontinuous on
$\mathfrak M\times \mathfrak M$
. The extended function is lower semicontinuous on
![]() $\mathfrak M\times \mathfrak M$
(see [Reference Hoffman10, Theorem 6.2]) and determines a metric on
$\mathfrak M\times \mathfrak M$
(see [Reference Hoffman10, Theorem 6.2]) and determines a metric on
![]() $\mathfrak M$
with the property that any two open balls of radius
$\mathfrak M$
with the property that any two open balls of radius
![]() $1$
are either equal or disjoint. The Gleason part of
$1$
are either equal or disjoint. The Gleason part of
![]() $m\in \mathfrak M$
is then defined by
$m\in \mathfrak M$
is then defined by
![]() $P(m):=\{m'\in \mathfrak M\, :\, \rho (m',m)<1\}$
. Hoffman’s classification of Gleason parts [Reference Hoffman10] shows that there are only two cases: either
$P(m):=\{m'\in \mathfrak M\, :\, \rho (m',m)<1\}$
. Hoffman’s classification of Gleason parts [Reference Hoffman10] shows that there are only two cases: either
![]() $P(m)=\{m\}$
or
$P(m)=\{m\}$
or
![]() $P(m)$
is an analytic disk. The latter case means that there is a parameterization of
$P(m)$
is an analytic disk. The latter case means that there is a parameterization of
![]() $P(m)$
, i.e., a continuous one-to-one and onto map
$P(m)$
, i.e., a continuous one-to-one and onto map
![]() $L:\mathbb {D}\to P(m)$
such that
$L:\mathbb {D}\to P(m)$
such that
![]() $\hat f\circ L\in H^\infty $
for every
$\hat f\circ L\in H^\infty $
for every
![]() $f\in H^\infty $
. By
$f\in H^\infty $
. By
![]() $\mathfrak M_a$
we denote the union of all nontrivial (analytic disks) Gleason parts of
$\mathfrak M_a$
we denote the union of all nontrivial (analytic disks) Gleason parts of
![]() $\mathfrak M$
. It is known that
$\mathfrak M$
. It is known that
![]() $\mathfrak M_a\subset \mathfrak M$
is open and
$\mathfrak M_a\subset \mathfrak M$
is open and
![]() $P(m)\subset \mathfrak M_a$
if and only if m belongs to the closure of an interpolating sequence for
$P(m)\subset \mathfrak M_a$
if and only if m belongs to the closure of an interpolating sequence for
![]() $H^\infty $
.
$H^\infty $
.
For a Gleason part
![]() $ P\subset \mathfrak M_a\setminus \mathbb {D}$
, consider the closed ideal
$ P\subset \mathfrak M_a\setminus \mathbb {D}$
, consider the closed ideal
![]() $I_P =\{f\in H^\infty : \hat f \equiv 0 \textrm { on }P \}$
. According to Gorkin [Reference Gorkin9], the quotient Banach algebra
$I_P =\{f\in H^\infty : \hat f \equiv 0 \textrm { on }P \}$
. According to Gorkin [Reference Gorkin9], the quotient Banach algebra
![]() $H^\infty /I_P$
is semisimple with maximal ideal space
$H^\infty /I_P$
is semisimple with maximal ideal space
![]() $\bar P$
(- the closure of P in
$\bar P$
(- the closure of P in
![]() $\mathfrak M$
). The corresponding Gelfand transform maps
$\mathfrak M$
). The corresponding Gelfand transform maps
![]() $f+I_P\in H^\infty /I_P$
to
$f+I_P\in H^\infty /I_P$
to
![]() $\hat f|_{\bar P}\in C(\bar P)$
. In [Reference Suárez15, Reference Suárez16], Suárez proved that the Gelfand transform maps
$\hat f|_{\bar P}\in C(\bar P)$
. In [Reference Suárez15, Reference Suárez16], Suárez proved that the Gelfand transform maps
![]() $H^\infty /I_P$
isomorphically onto the closed subalgebra
$H^\infty /I_P$
isomorphically onto the closed subalgebra
![]() $\mathcal O( \bar P)$
of functions
$\mathcal O( \bar P)$
of functions
![]() $g\in C(\bar P)$
such that
$g\in C(\bar P)$
such that
![]() $g\circ L\in H^\infty $
, where L is a parameterization of P. Specifically, he proved the following interpolation result.
$g\circ L\in H^\infty $
, where L is a parameterization of P. Specifically, he proved the following interpolation result.
Theorem A There is an absolute constant
![]() $C\ge 1$
such that for every
$C\ge 1$
such that for every
![]() $g\in \mathcal O( \bar P)$
, there exists
$g\in \mathcal O( \bar P)$
, there exists
![]() $f\in H^\infty $
such that
$f\in H^\infty $
such that
(Here and below for a normed space X, its norm is denoted by
![]() $\lVert \cdot \rVert _X$
.)
$\lVert \cdot \rVert _X$
.)
In the framework of the Stein-like theory on
![]() $\mathfrak M$
developed in [Reference Brudnyi2] analogous to the classical theory of complex functions on Stein spaces, and taking into account the results of Suárez,
$\mathfrak M$
developed in [Reference Brudnyi2] analogous to the classical theory of complex functions on Stein spaces, and taking into account the results of Suárez,
![]() $\bar P$
can be viewed as an analog of a complex connected submanifold of
$\bar P$
can be viewed as an analog of a complex connected submanifold of
![]() $\mathfrak M$
, and
$\mathfrak M$
, and
![]() $\mathcal O(\bar P)$
as an analog of the space of holomorphic functions on
$\mathcal O(\bar P)$
as an analog of the space of holomorphic functions on
![]() $\bar P$
. Following this line, and using recent advances from the author’s work [Reference Brudnyi3, Reference Brudnyi4], in this paper we will prove analogs of Theorem A for such functions on
$\bar P$
. Following this line, and using recent advances from the author’s work [Reference Brudnyi3, Reference Brudnyi4], in this paper we will prove analogs of Theorem A for such functions on
![]() $\bar P$
with values in complex Banach spaces and in some complex submanifolds of
$\bar P$
with values in complex Banach spaces and in some complex submanifolds of
![]() ${\mathbb C}^n$
. Our results are related to some general interpolation results obtained previously in [Reference Brudnyi2, Theorem 1.9] and [Reference Brudnyi3, Theorem 1.11].
${\mathbb C}^n$
. Our results are related to some general interpolation results obtained previously in [Reference Brudnyi2, Theorem 1.9] and [Reference Brudnyi3, Theorem 1.11].
1.2
Our first result extends Theorem A to the case of Banach-valued functions.
Let X be a complex Banach space, and let
![]() $V\subset \mathbb {D}$
be an open subset. We denote by
$V\subset \mathbb {D}$
be an open subset. We denote by
![]() $H_{\mathrm {comp }}^\infty (V,X)$
the Banach space of X-valued holomorphic functions f on V with relatively compact images equipped with norm
$H_{\mathrm {comp }}^\infty (V,X)$
the Banach space of X-valued holomorphic functions f on V with relatively compact images equipped with norm
![]() $\|f\|_{H_{\mathrm {comp }}^\infty (V,X)}:=\sup _{z\in V}\|f(z)\|_X$
. If
$\|f\|_{H_{\mathrm {comp }}^\infty (V,X)}:=\sup _{z\in V}\|f(z)\|_X$
. If
![]() $V=\mathbb {D}\cap \widehat V$
for an open set
$V=\mathbb {D}\cap \widehat V$
for an open set
![]() $\widehat V\subset \mathfrak M$
, then every function
$\widehat V\subset \mathfrak M$
, then every function
![]() $f\in H_{\mathrm {comp }}^\infty (V,X)$
extends to a function with a relatively compact image
$f\in H_{\mathrm {comp }}^\infty (V,X)$
extends to a function with a relatively compact image
![]() $\hat f\in C(\widehat V,X)$
(see [Reference Suárez14, Theorem 3.2] and [Reference Brudnyi2, Proposition 1.3]). Let
$\hat f\in C(\widehat V,X)$
(see [Reference Suárez14, Theorem 3.2] and [Reference Brudnyi2, Proposition 1.3]). Let
![]() $P\subset \mathfrak M_a$
be a Gleason part with a parameterization
$P\subset \mathfrak M_a$
be a Gleason part with a parameterization
![]() $L:\mathbb {D}\to P$
. We denote by
$L:\mathbb {D}\to P$
. We denote by
![]() $\mathcal O(\bar P,X)\subset C(\bar P, X)$
the Banach subspace of continuous X-valued functions g on
$\mathcal O(\bar P,X)\subset C(\bar P, X)$
the Banach subspace of continuous X-valued functions g on
![]() $\bar P$
such that
$\bar P$
such that
![]() $g\circ L$
is a holomorphic X-valued function on
$g\circ L$
is a holomorphic X-valued function on
![]() $\mathbb {D}$
with norm
$\mathbb {D}$
with norm
![]() $\|g\|_{C(\bar P, X)}:=\sup _{x\in \bar P}\|g(x)\|_X$
.
$\|g\|_{C(\bar P, X)}:=\sup _{x\in \bar P}\|g(x)\|_X$
.
Theorem 1.1 There is an absolute constant
![]() $C\ge 1$
such that for every
$C\ge 1$
such that for every
![]() $g\in \mathcal O(\bar P,X)$
, there exists
$g\in \mathcal O(\bar P,X)$
, there exists
![]() $f\in H_{\mathrm {comp }}^\infty (\mathbb {D},X)$
such that
$f\in H_{\mathrm {comp }}^\infty (\mathbb {D},X)$
such that
It was established in [Reference Suárez15, Theorem 4.1] that if the Gleason part P is a homeomorphic disk, i.e., if a parameterization
![]() $L:\mathbb {D}\to \mathfrak M$
of P is an embedding, then Theorem A is valid with constant
$L:\mathbb {D}\to \mathfrak M$
of P is an embedding, then Theorem A is valid with constant
![]() $C=1$
. So it is natural to ask whether this would also be true in the case of Theorem 1.1.
$C=1$
. So it is natural to ask whether this would also be true in the case of Theorem 1.1.
To formulate our second result, let us recall the following definitions.
![]() $(\triangledown )$
A complex manifold
$(\triangledown )$
A complex manifold
![]() $\mathcal M$
is said to be Oka if every holomorphic map
$\mathcal M$
is said to be Oka if every holomorphic map
![]() $f: K\rightarrow \mathcal M$
from a neighborhood of a compact convex set
$f: K\rightarrow \mathcal M$
from a neighborhood of a compact convex set
![]() $K \subset {\mathbb C}^k$
,
$K \subset {\mathbb C}^k$
,
![]() $k\in \mathbb {N}$
, can be approximated uniformly on K by entire maps
$k\in \mathbb {N}$
, can be approximated uniformly on K by entire maps
![]() ${\mathbb C}^k\rightarrow \mathcal M$
.
${\mathbb C}^k\rightarrow \mathcal M$
.
We refer to the book [Reference Forstnerič7] and the paper [Reference Kusakabe13] for examples and basic results of the theory of Oka manifolds.
![]() $(\triangledown )$
A path-connected topological space X is i-simple if for each
$(\triangledown )$
A path-connected topological space X is i-simple if for each
![]() $x\in X$
the fundamental group
$x\in X$
the fundamental group
![]() $\pi _1(X,x_0)$
acts trivially on the i-homotopy group
$\pi _1(X,x_0)$
acts trivially on the i-homotopy group
![]() $\pi _i(X,x)$
(see, e.g., [Reference Hu12, Chapter IV.16] for the corresponding definitions and results).
$\pi _i(X,x)$
(see, e.g., [Reference Hu12, Chapter IV.16] for the corresponding definitions and results).
For instance, X is i-simple if the group
![]() $\pi _i(X)$
is trivial and
$\pi _i(X)$
is trivial and
![]() $1$
-simple if and only if the group
$1$
-simple if and only if the group
![]() $\pi _1(X)$
is abelian. Also, every path-connected topological group is i-simple for all i. The same is true for a complex manifold biholomorphic to the quotient of a connected complex Lie group by a connected closed Lie subgroup (see, e.g., [Reference Hu11, (3.2)]).
$\pi _1(X)$
is abelian. Also, every path-connected topological group is i-simple for all i. The same is true for a complex manifold biholomorphic to the quotient of a connected complex Lie group by a connected closed Lie subgroup (see, e.g., [Reference Hu11, (3.2)]).
Let
![]() $ \mathcal M$
be a complex manifold, and let
$ \mathcal M$
be a complex manifold, and let
![]() $P\subset \mathfrak M_a$
be a Gleason part with parameterization
$P\subset \mathfrak M_a$
be a Gleason part with parameterization
![]() $L:\mathbb {D}\to P$
. A continuous map
$L:\mathbb {D}\to P$
. A continuous map
![]() $F\in C(\bar P,\mathcal M)$
is said to be holomorphic (written,
$F\in C(\bar P,\mathcal M)$
is said to be holomorphic (written,
![]() $F\in \mathcal O(\bar P ,\mathcal M)$
) if
$F\in \mathcal O(\bar P ,\mathcal M)$
) if
![]() $F\circ L:\mathbb {D}\to \mathcal M$
is a holomorphic map of complex manifolds.
$F\circ L:\mathbb {D}\to \mathcal M$
is a holomorphic map of complex manifolds.
Let
![]() $\mathscr {O}$
be the class of connected Oka manifolds
$\mathscr {O}$
be the class of connected Oka manifolds
![]() $\mathcal M$
embeddable as complex submanifolds into complex Euclidean spaces and having i-simple for
$\mathcal M$
embeddable as complex submanifolds into complex Euclidean spaces and having i-simple for
![]() $i=1,2$
finite unbranched coverings. The analog of Theorem A for holomorphic maps with values in manifolds of class
$i=1,2$
finite unbranched coverings. The analog of Theorem A for holomorphic maps with values in manifolds of class
![]() $\mathscr {O}$
is as follows:
$\mathscr {O}$
is as follows:
Theorem 1.2 Let
![]() $\mathcal M\subset {\mathbb C}^n$
be of class
$\mathcal M\subset {\mathbb C}^n$
be of class
![]() $\mathscr {O}$
, and let K be a compact subset of
$\mathscr {O}$
, and let K be a compact subset of
![]() $\mathcal M$
. There is a constant
$\mathcal M$
. There is a constant
![]() $C=C(\mathcal M,K,n)$
Footnote
1
such that for every map
$C=C(\mathcal M,K,n)$
Footnote
1
such that for every map
![]() $F\in \mathcal O (\bar P,\mathcal M)$
with image in K, there exists a map
$F\in \mathcal O (\bar P,\mathcal M)$
with image in K, there exists a map
![]() $G=(g_1,\dots , g_n)\in (H^\infty )^n\subset C(\mathbb {D},{\mathbb C}^n)$
with a relatively compact image in
$G=(g_1,\dots , g_n)\in (H^\infty )^n\subset C(\mathbb {D},{\mathbb C}^n)$
with a relatively compact image in
![]() $\mathcal M$
such that
$\mathcal M$
such that
Here,
![]() $\widehat G:=(\hat g_1,\dots ,\hat g_n)$
.
$\widehat G:=(\hat g_1,\dots ,\hat g_n)$
.
Remark 1.3 (1) The class
![]() $\mathscr {O}$
was originally introduced in [Reference Brudnyi3] in connection with Theorem 1.6 of that paper. The proof of this theorem invokes an extension result for continuous maps defined on certain subsets of the maximal ideal space of the algebra
$\mathscr {O}$
was originally introduced in [Reference Brudnyi3] in connection with Theorem 1.6 of that paper. The proof of this theorem invokes an extension result for continuous maps defined on certain subsets of the maximal ideal space of the algebra
![]() $H^\infty (\mathbb {D}\times \mathbb {N})$
. The extension result is obtained using some obstruction theory and depends on the fact that the covering dimension of the maximal ideal space
$H^\infty (\mathbb {D}\times \mathbb {N})$
. The extension result is obtained using some obstruction theory and depends on the fact that the covering dimension of the maximal ideal space
![]() $\mathfrak M(H^\infty (\mathbb {D}\times \mathbb {N}))$
is
$\mathfrak M(H^\infty (\mathbb {D}\times \mathbb {N}))$
is
![]() $2$
and on the i-simplicity for
$2$
and on the i-simplicity for
![]() $i=1,2$
of manifolds of class
$i=1,2$
of manifolds of class
![]() $\mathscr {O}$
.
$\mathscr {O}$
.
(2) The class
![]() $\mathscr {O}$
contains, e.g.,
$\mathscr {O}$
contains, e.g.,
![]() $\bullet $
complements in
$\bullet $
complements in
![]() ${\mathbb C}^k$
,
${\mathbb C}^k$
,
![]() $k>1$
, of complex algebraic subvarieties of codimension
$k>1$
, of complex algebraic subvarieties of codimension
![]() $\ge \ 2$
and of compact polynomially convex sets (these manifolds are simply connected; see [Reference Forstnerič6]);
$\ge \ 2$
and of compact polynomially convex sets (these manifolds are simply connected; see [Reference Forstnerič6]);
![]() $\bullet $
connected Stein Lie groups;
$\bullet $
connected Stein Lie groups;
![]() $\bullet $
quotients of connected reductive complex Lie groups by Zariski closed subgroups (these manifolds are quasi-affine algebraic (see, e.g., [Reference Akhiezer, Gindikin and Khenkin1, Theorem 5.6] for the references); they have i-simple finite unbranched coverings because Zariski closed subgroups have finitely many connected components and quotients of connected complex Lie groups by connected closed Lie subgroups are i-simple for all i (see, e.g., [Reference Hu11, (3.2)])). Also, direct products of manifolds from class
$\bullet $
quotients of connected reductive complex Lie groups by Zariski closed subgroups (these manifolds are quasi-affine algebraic (see, e.g., [Reference Akhiezer, Gindikin and Khenkin1, Theorem 5.6] for the references); they have i-simple finite unbranched coverings because Zariski closed subgroups have finitely many connected components and quotients of connected complex Lie groups by connected closed Lie subgroups are i-simple for all i (see, e.g., [Reference Hu11, (3.2)])). Also, direct products of manifolds from class
![]() $\mathscr {O}$
belong to
$\mathscr {O}$
belong to
![]() $\mathscr {O}$
and so forth.
$\mathscr {O}$
and so forth.
2 Auxiliary results
A subset S of a metric space
![]() $(\mathcal M,d)$
is said to be
$(\mathcal M,d)$
is said to be
![]() $\epsilon $
-separated if
$\epsilon $
-separated if
![]() $d(x,y)\ge \epsilon $
for all
$d(x,y)\ge \epsilon $
for all
![]() $x, y\in S$
,
$x, y\in S$
,
![]() $x\ne y$
. A maximal
$x\ne y$
. A maximal
![]() $\epsilon $
-separated subset of
$\epsilon $
-separated subset of
![]() $\mathcal M$
is said to be an
$\mathcal M$
is said to be an
![]() $\epsilon $
-chain. Thus, if
$\epsilon $
-chain. Thus, if
![]() $S\subset \mathcal M$
is an
$S\subset \mathcal M$
is an
![]() $\epsilon $
-chain, then S is
$\epsilon $
-chain, then S is
![]() $\epsilon $
-separated and for every
$\epsilon $
-separated and for every
![]() $z\in \mathcal M\setminus S$
there is an
$z\in \mathcal M\setminus S$
there is an
![]() $x\in S$
such that
$x\in S$
such that
![]() $d(z,x)<\epsilon $
. The existence of
$d(z,x)<\epsilon $
. The existence of
![]() $\epsilon $
-chains follows from the Zorn lemma.
$\epsilon $
-chains follows from the Zorn lemma.
A subset
![]() $S\subset \mathbb {D}$
is said to be quasi-interpolating, if an
$S\subset \mathbb {D}$
is said to be quasi-interpolating, if an
![]() $\epsilon $
-chain of S,
$\epsilon $
-chain of S,
![]() $\epsilon \in (0,1)$
, with respect to the pseudohyperbolic metric
$\epsilon \in (0,1)$
, with respect to the pseudohyperbolic metric
![]() $\rho $
(see (1.1)) is an interpolating sequence for
$\rho $
(see (1.1)) is an interpolating sequence for
![]() $H^\infty $
. (In fact, in this case, every
$H^\infty $
. (In fact, in this case, every
![]() $\epsilon $
-chain of S,
$\epsilon $
-chain of S,
![]() $\epsilon \in (0,1)$
, with respect to
$\epsilon \in (0,1)$
, with respect to
![]() $\rho $
is an interpolating sequence for
$\rho $
is an interpolating sequence for
![]() $H^\infty $
; this easily follows from [Reference Garnett8, Chapter X, Corollary 1.6, Chapter VII, Lemma 5.3].)
$H^\infty $
; this easily follows from [Reference Garnett8, Chapter X, Corollary 1.6, Chapter VII, Lemma 5.3].)
Let
![]() $K\subset \mathbb {D}$
be a Lebesgue measurable subset, and let X be a complex Banach space. Two X-valued functions on
$K\subset \mathbb {D}$
be a Lebesgue measurable subset, and let X be a complex Banach space. Two X-valued functions on
![]() $\mathbb {D}$
are equivalent if they coincide a.e. on
$\mathbb {D}$
are equivalent if they coincide a.e. on
![]() $\mathbb {D}$
. The complex Banach space
$\mathbb {D}$
. The complex Banach space
![]() $L^\infty (K,X)$
consists of equivalence classes of Bochner measurable essentially bounded functions
$L^\infty (K,X)$
consists of equivalence classes of Bochner measurable essentially bounded functions
![]() $f:\mathbb {D}\to X$
equal
$f:\mathbb {D}\to X$
equal
![]() $0$
a.e. on
$0$
a.e. on
![]() $\mathbb {D}\setminus K$
equipped with norm
$\mathbb {D}\setminus K$
equipped with norm
![]() $\|f\|_{L^\infty (K,X)}:=\mathrm { ess}\sup _{z\in K}\|f(z)\|_X$
. Also, we denote by
$\|f\|_{L^\infty (K,X)}:=\mathrm { ess}\sup _{z\in K}\|f(z)\|_X$
. Also, we denote by
![]() $C_\rho (\mathbb {D},X)$
the Banach space of bounded continuous functions
$C_\rho (\mathbb {D},X)$
the Banach space of bounded continuous functions
![]() $f:\mathbb {D}\rightarrow X$
uniformly continuous with respect to
$f:\mathbb {D}\rightarrow X$
uniformly continuous with respect to
![]() $\rho $
equipped with norm
$\rho $
equipped with norm
![]() $\|f\|_{C_\rho (\mathbb {D},X)}:=\sup _{z\in \mathbb {D}}\|f(z)\|_X$
.
$\|f\|_{C_\rho (\mathbb {D},X)}:=\sup _{z\in \mathbb {D}}\|f(z)\|_X$
.
In [Reference Brudnyi4], we studied the differential equation
We proved that if K is quasi-interpolating, then equation (2.1) has a weak solution
![]() $F\in C_\rho (\mathbb {D},X)$
, i.e., such that for every
$F\in C_\rho (\mathbb {D},X)$
, i.e., such that for every
![]() $C^\infty $
function s with compact support in
$C^\infty $
function s with compact support in
![]() $\mathbb {D}$
,
$\mathbb {D}$
,
 $$ \begin{align} \iint \limits_{\mathbb{D}}F(z)\cdot\frac{\partial s(z)}{\partial\bar{z}}\,dz\wedge d\bar{z}=-\iint\limits_{\mathbb{D}}\frac{f(z)}{1-|z|^2}\,\cdot s(z)\,dz\wedge d\bar{z}, \end{align} $$
$$ \begin{align} \iint \limits_{\mathbb{D}}F(z)\cdot\frac{\partial s(z)}{\partial\bar{z}}\,dz\wedge d\bar{z}=-\iint\limits_{\mathbb{D}}\frac{f(z)}{1-|z|^2}\,\cdot s(z)\,dz\wedge d\bar{z}, \end{align} $$
given by a bounded linear operator
![]() $L_K^X: L^\infty (K,X)\rightarrow C_\rho (\mathbb {D},X)$
. Specifically, we obtained the following result.
$L_K^X: L^\infty (K,X)\rightarrow C_\rho (\mathbb {D},X)$
. Specifically, we obtained the following result.
Theorem 2.1 [Reference Brudnyi4, Theorem 1.1]
Suppose a quasi-interpolating set
![]() $K\subset \mathbb {D}$
is Lebesgue measurable and
$K\subset \mathbb {D}$
is Lebesgue measurable and
![]() $\zeta =\{z_j\}$
is an
$\zeta =\{z_j\}$
is an
![]() $\epsilon $
-chain of K,
$\epsilon $
-chain of K,
![]() $\epsilon \in (0,1)$
, with respect to
$\epsilon \in (0,1)$
, with respect to
![]() $\rho $
such that
$\rho $
such that
There is a bounded linear operator
![]() $L_K^X: L^\infty (K,X)\to C_\rho (\mathbb {D},X)$
of norm
$L_K^X: L^\infty (K,X)\to C_\rho (\mathbb {D},X)$
of norm
 $$ \begin{align} \|L_K^X\|\le \frac{c\epsilon}{1-\epsilon}\cdot\max\left\{1,\frac{\log\frac{1}{\delta}}{(1-\epsilon_*)^2}\right\},\quad \epsilon_*:=\max\left\{\frac 1 2,\epsilon\right\}, \end{align} $$
$$ \begin{align} \|L_K^X\|\le \frac{c\epsilon}{1-\epsilon}\cdot\max\left\{1,\frac{\log\frac{1}{\delta}}{(1-\epsilon_*)^2}\right\},\quad \epsilon_*:=\max\left\{\frac 1 2,\epsilon\right\}, \end{align} $$
for a numerical constant
![]() $c<5^2\times 10^6$
such that for every
$c<5^2\times 10^6$
such that for every
![]() $f\in L^\infty (K,X)$
the function
$f\in L^\infty (K,X)$
the function
![]() $L_K^X f$
is a weak solution of equation (2.1).
$L_K^X f$
is a weak solution of equation (2.1).
The operator
![]() $L_K^X$
has the following properties:
$L_K^X$
has the following properties:
-
(i) If
 $T: X\rightarrow Y$
is a bounded linear operator between complex Banach spaces, then where
$T: X\rightarrow Y$
is a bounded linear operator between complex Banach spaces, then where $$\begin{align*}TL_K^X=L_K^Y T, \end{align*}$$
$$\begin{align*}TL_K^X=L_K^Y T, \end{align*}$$
 $(Tf)(z):=T(f(z))$
,
$(Tf)(z):=T(f(z))$
,
 $z\in \mathbb {D}$
,
$z\in \mathbb {D}$
,
 $f:\mathbb {D}\to X$
.
$f:\mathbb {D}\to X$
.
-
(ii) If
 $f\in L^\infty (K,X)$
has a compact essential range, then the range of
$f\in L^\infty (K,X)$
has a compact essential range, then the range of
 $L_K^X f$
is relatively compact.
$L_K^X f$
is relatively compact. -
(iii) If
 $f\in L^\infty (X,K)$
is continuously differentiable on an open set
$f\in L^\infty (X,K)$
is continuously differentiable on an open set
 $U\subset \mathbb {D}$
, then
$U\subset \mathbb {D}$
, then
 $L_K^X f$
is continuously differentiable on U.
$L_K^X f$
is continuously differentiable on U.
An important example of a quasi-interpolating set is a pseudohyperbolic neighborhood of a Carleson contour used in the proof of the corona theorem. In particular, using the construction from the proof of the theorem, one obtains the following (for the proof of this result, see [Reference Carleson5, Reference Ziskind17] and [Reference Garnett8, Chapter VIII.5]).
Lemma 2.2 Suppose
![]() $f\in H^\infty $
with
$f\in H^\infty $
with
![]() $\|f\|_{\infty }\le 1$
. Given
$\|f\|_{\infty }\le 1$
. Given
![]() $0<\beta <1$
, there is an
$0<\beta <1$
, there is an
![]() $\varepsilon =\varepsilon (\beta )\in (0,\beta )$
, a quasi-interpolating set
$\varepsilon =\varepsilon (\beta )\in (0,\beta )$
, a quasi-interpolating set
![]() $K_\beta \subset \mathbb {D}$
having a
$K_\beta \subset \mathbb {D}$
having a
![]() $\frac 12$
-chain
$\frac 12$
-chain
![]() $ \zeta \subset K_\beta $
such that
$ \zeta \subset K_\beta $
such that
![]() $\delta (\zeta )\ge \delta =\delta (\beta )>0$
, and a function
$\delta (\zeta )\ge \delta =\delta (\beta )>0$
, and a function
![]() $\Phi \in C^\infty (\mathbb {D})$
,
$\Phi \in C^\infty (\mathbb {D})$
,
![]() $0\le \Phi \le 1$
, satisfying
$0\le \Phi \le 1$
, satisfying
![]() $\mathbb {D}\setminus K_\beta \subset \Phi ^{-1}(\{0,1\})$
and
$\mathbb {D}\setminus K_\beta \subset \Phi ^{-1}(\{0,1\})$
and
-
(i)
 $$\begin{align*}\{z\in\mathbb{D}\, :\, |f(z)|\ge\beta\}\subset \Phi^{-1}(0)\cap (\mathbb{D}\setminus K_\beta); \end{align*}$$
$$\begin{align*}\{z\in\mathbb{D}\, :\, |f(z)|\ge\beta\}\subset \Phi^{-1}(0)\cap (\mathbb{D}\setminus K_\beta); \end{align*}$$
-
(ii)
 $$\begin{align*}\{z\in\mathbb{D}\, :\, |f(z)|\le\varepsilon\}\subset \Phi^{-1}(1)\cap (\mathbb{D}\setminus K_\beta);\end{align*}$$
$$\begin{align*}\{z\in\mathbb{D}\, :\, |f(z)|\le\varepsilon\}\subset \Phi^{-1}(1)\cap (\mathbb{D}\setminus K_\beta);\end{align*}$$
-
(iii)
 $$\begin{align*}\frac{\partial\Phi}{\partial\bar z}=\frac{g(z)}{1-|z|^2},\ \ z\in\mathbb{D},\quad\textrm{where}\quad g\in L^\infty(K_\beta,{\mathbb C}),\ \ \|g\|_\infty\le A=A(\beta). \end{align*}$$
$$\begin{align*}\frac{\partial\Phi}{\partial\bar z}=\frac{g(z)}{1-|z|^2},\ \ z\in\mathbb{D},\quad\textrm{where}\quad g\in L^\infty(K_\beta,{\mathbb C}),\ \ \|g\|_\infty\le A=A(\beta). \end{align*}$$
Using the previous results, we prove the following Banach-valued version of [Reference Suárez16, Lemma 3.9].
Lemma 2.3 Let X be a complex Banach space, let u be an inner function, and let
![]() $0<\beta <1$
. Put
$0<\beta <1$
. Put
![]() $V=\{z\in \mathbb {D}\, :\, |u(z)|<\beta \}$
and suppose that
$V=\{z\in \mathbb {D}\, :\, |u(z)|<\beta \}$
and suppose that
![]() $g\in H^\infty _{\mathrm {comp}}(V,X)$
. Then there are
$g\in H^\infty _{\mathrm {comp}}(V,X)$
. Then there are
![]() $\varepsilon =\varepsilon (\beta )\in (0,\beta )$
,
$\varepsilon =\varepsilon (\beta )\in (0,\beta )$
,
![]() $C=C(\beta )>0$
, and
$C=C(\beta )>0$
, and
![]() $G\in H_{\mathrm {comp}}^\infty (\mathbb {D},X)$
such that
$G\in H_{\mathrm {comp}}^\infty (\mathbb {D},X)$
such that
-
(i)
 $$\begin{align*}\|G\|_{H_{\mathrm{comp}}^\infty(\mathbb{D},X)}\le C\|g\|_{H_{\mathrm{comp}}^\infty(V,X)}\quad \textrm{and} \end{align*}$$
$$\begin{align*}\|G\|_{H_{\mathrm{comp}}^\infty(\mathbb{D},X)}\le C\|g\|_{H_{\mathrm{comp}}^\infty(V,X)}\quad \textrm{and} \end{align*}$$
-
(ii)
 $$\begin{align*}|G(z)-g(z)|\le C\|g\|_{H_{\mathrm{comp}}^\infty(V,X)} |u(z)|\ \textrm{when}\ |u(z)|<\varepsilon. \end{align*}$$
$$\begin{align*}|G(z)-g(z)|\le C\|g\|_{H_{\mathrm{comp}}^\infty(V,X)} |u(z)|\ \textrm{when}\ |u(z)|<\varepsilon. \end{align*}$$
Proof We choose
![]() $\Phi $
of Lemma 2.2 for the function
$\Phi $
of Lemma 2.2 for the function
![]() $f:=u$
. According to Lemma 2.2(ii) and (iii) and Theorem 2.1(ii) and (iii), there is a function with relatively compact image
$f:=u$
. According to Lemma 2.2(ii) and (iii) and Theorem 2.1(ii) and (iii), there is a function with relatively compact image
![]() $F\in C^\infty (\mathbb {D},X)$
such that for some
$F\in C^\infty (\mathbb {D},X)$
such that for some
![]() $c=c(\beta )>0$
,
$c=c(\beta )>0$
,
(Note that
![]() $\frac {g}{u}\frac {\partial \Phi }{\partial \bar z}\in L^\infty (K_\beta ,X)$
and has a relatively compact image.)
$\frac {g}{u}\frac {\partial \Phi }{\partial \bar z}\in L^\infty (K_\beta ,X)$
and has a relatively compact image.)
Consider the function
![]() $G=g\Phi -Fu$
. Then the previous equation implies
$G=g\Phi -Fu$
. Then the previous equation implies
![]() $\frac {\partial G}{\partial \bar z}=0$
, i.e.,
$\frac {\partial G}{\partial \bar z}=0$
, i.e.,
![]() $G\in H^\infty _{\mathrm {comp}}(\mathbb {D},X)$
and by Lemma 2.2(i) (since
$G\in H^\infty _{\mathrm {comp}}(\mathbb {D},X)$
and by Lemma 2.2(i) (since
![]() $\lim _{r\to 1^{-}} |u(re^{i\theta })|=1$
a.e.
$\lim _{r\to 1^{-}} |u(re^{i\theta })|=1$
a.e.
![]() $\theta \in [0,2\pi )$
),
$\theta \in [0,2\pi )$
),
On the other hand, Lemma 2.2(ii) implies that
![]() $G(z)=g(z)- F(z)u(z)$
when
$G(z)=g(z)- F(z)u(z)$
when
![]() $|u(z)|<\varepsilon $
. Thus, for such z,
$|u(z)|<\varepsilon $
. Thus, for such z,
3 Proofs
Proof of Theorem 1.1
The construction presented in [Reference Suárez16, Section 4] is also applicable to maps
![]() $g\in \mathcal O(\bar P,X)$
. In particular, one can define an open set
$g\in \mathcal O(\bar P,X)$
. In particular, one can define an open set
![]() $\Omega \subset \mathbb {D}$
, a Blaschke product
$\Omega \subset \mathbb {D}$
, a Blaschke product
![]() $b\in H^\infty $
, such that
$b\in H^\infty $
, such that
![]() $\hat b= 0$
on
$\hat b= 0$
on
![]() $\bar P$
and
$\bar P$
and
![]() $V=\{z\in \mathbb {D}\, :\, |b(z)|<\frac 12\}\subset \Omega $
, and a function
$V=\{z\in \mathbb {D}\, :\, |b(z)|<\frac 12\}\subset \Omega $
, and a function
![]() $h\in H_{\mathrm {comp}}(\Omega ,X)$
whose image is contained in the image of
$h\in H_{\mathrm {comp}}(\Omega ,X)$
whose image is contained in the image of
![]() $g|_P$
such that for every point
$g|_P$
such that for every point
![]() $x\in P$
and a net
$x\in P$
and a net
![]() $\{z_\alpha \}\subset \mathbb {D}$
converging to x,
$\{z_\alpha \}\subset \mathbb {D}$
converging to x,
Since V is the intersection of
![]() $\mathbb {D}$
and the open set
$\mathbb {D}$
and the open set
![]() $\widehat V:=\{x\in \mathfrak M\, :\ |\hat b(x)|<\frac 1 2\}\subset \mathfrak M$
, the function h extends to a continuous X-valued function
$\widehat V:=\{x\in \mathfrak M\, :\ |\hat b(x)|<\frac 1 2\}\subset \mathfrak M$
, the function h extends to a continuous X-valued function
![]() $\hat h$
with a relatively compact image on
$\hat h$
with a relatively compact image on
![]() $\widehat V$
(see [Reference Suárez14, Theorem 3.2] and [Reference Brudnyi2, Proposition 1.3]). By (3.1) and the definition of h,
$\widehat V$
(see [Reference Suárez14, Theorem 3.2] and [Reference Brudnyi2, Proposition 1.3]). By (3.1) and the definition of h,
Further, we apply Lemma 2.3 to the inner function b and the function
![]() $h\in H_{\mathrm {comp}}^\infty (V,X)$
with
$h\in H_{\mathrm {comp}}^\infty (V,X)$
with
![]() $\beta =\frac 12$
. Then, due to (3.2), we get absolute constants
$\beta =\frac 12$
. Then, due to (3.2), we get absolute constants
![]() $C>0$
and
$C>0$
and
![]() $\varepsilon \in (0,\frac 12)$
, and a function
$\varepsilon \in (0,\frac 12)$
, and a function
![]() $f\in H_{\mathrm {comp}}^\infty (\mathbb {D},X)$
such that
$f\in H_{\mathrm {comp}}^\infty (\mathbb {D},X)$
such that
and
Since
![]() $\hat b= 0$
on
$\hat b= 0$
on
![]() $\bar P$
, the latter inequality and (3.2) imply
$\bar P$
, the latter inequality and (3.2) imply
as required.
Proof of Theorem 1.2
Let
![]() $F\in \mathcal O (\bar P,\mathcal M)$
have an image in K. According to Theorem 1.1, there is a map
$F\in \mathcal O (\bar P,\mathcal M)$
have an image in K. According to Theorem 1.1, there is a map
![]() $F_1\in (H^\infty )^n$
such that
$F_1\in (H^\infty )^n$
such that
Further, as in the previous proof, one applies a construction from [Reference Suárez16, Section 4] to define an open set
![]() $\Omega \subset \mathbb {D}$
, a Blaschke product
$\Omega \subset \mathbb {D}$
, a Blaschke product
![]() $b\in H^\infty $
, such that
$b\in H^\infty $
, such that
![]() $\hat b= 0$
on
$\hat b= 0$
on
![]() $\bar P$
and
$\bar P$
and
![]() $V=\{z\in \mathbb {D}\, :\, |b(z)|<\frac 12\}\subset \Omega $
, and a holomorphic map
$V=\{z\in \mathbb {D}\, :\, |b(z)|<\frac 12\}\subset \Omega $
, and a holomorphic map
![]() $H\in H^\infty (\Omega ,\mathcal M)$
with image in K such that
$H\in H^\infty (\Omega ,\mathcal M)$
with image in K such that
Since
![]() $\mathcal M\in \mathscr {O}$
, conditions (3.3) and (3.4) allow us to apply [Reference Brudnyi3, Theorem 1.11] with
$\mathcal M\in \mathscr {O}$
, conditions (3.3) and (3.4) allow us to apply [Reference Brudnyi3, Theorem 1.11] with
![]() $c=2$
,
$c=2$
,
![]() $\delta =\frac 12$
,
$\delta =\frac 12$
,
![]() $k=1$
,
$k=1$
,
![]() $\Pi _{c,\delta }^k=\{z\in \mathbb {D}\, :\, |2b(z)|<\delta \}$
,
$\Pi _{c,\delta }^k=\{z\in \mathbb {D}\, :\, |2b(z)|<\delta \}$
,
![]() $\Pi _c^k=\Pi _{c,1}^k$
,
$\Pi _c^k=\Pi _{c,1}^k$
,
![]() $g=F_1$
,
$g=F_1$
,
![]() $b=C$
, and
$b=C$
, and
![]() $f=H$
to get a constant
$f=H$
to get a constant
![]() $C(\mathcal M,K,n):=C(\mathcal M,K,n,b,c,k,\delta )>1$
and a map
$C(\mathcal M,K,n):=C(\mathcal M,K,n,b,c,k,\delta )>1$
and a map
![]() $G\in (H^\infty )^n$
with a relatively compact image in
$G\in (H^\infty )^n$
with a relatively compact image in
![]() $\mathcal M$
such that
$\mathcal M$
such that
as required.
4 Concluding remark
Let
![]() $\mathfrak { M}^n$
be the n-fold direct product of
$\mathfrak { M}^n$
be the n-fold direct product of
![]() $\mathfrak {M}$
. For Gleason parts
$\mathfrak {M}$
. For Gleason parts
![]() $P_1,\dots , P_n\in \mathfrak M_a$
with parameterizations
$P_1,\dots , P_n\in \mathfrak M_a$
with parameterizations
![]() $L_1,\dots , L_n$
, we set
$L_1,\dots , L_n$
, we set
![]() $P:=P_1\times \cdots \times P_n\subset \mathfrak M_a^n$
and
$P:=P_1\times \cdots \times P_n\subset \mathfrak M_a^n$
and
![]() $L:=(L_1,\dots , L_n):=\mathbb D^n\to P$
. As before, for a complex Banach space X, we denote by
$L:=(L_1,\dots , L_n):=\mathbb D^n\to P$
. As before, for a complex Banach space X, we denote by
![]() $\mathcal O(\bar P,X)$
the Banach space of continuous X-valued maps f on the closure
$\mathcal O(\bar P,X)$
the Banach space of continuous X-valued maps f on the closure
![]() $\bar P\subset \mathfrak { M}^n$
of P such that
$\bar P\subset \mathfrak { M}^n$
of P such that
![]() $f\circ L\in H^\infty (\mathbb D^n,X)$
equipped with the norm
$f\circ L\in H^\infty (\mathbb D^n,X)$
equipped with the norm
![]() $\|f\|_{C(\bar P,X)}$
. Based on Theorem 1.1, we can prove formally a more general statement.
$\|f\|_{C(\bar P,X)}$
. Based on Theorem 1.1, we can prove formally a more general statement.
Theorem 4.1 For every
![]() $f\in \mathcal O(\bar P,X)$
, there is a map
$f\in \mathcal O(\bar P,X)$
, there is a map
![]() $F\in \mathcal O(\mathfrak M^n,X)$
such that
$F\in \mathcal O(\mathfrak M^n,X)$
such that
where C is the constant in Theorem 1.1.
Proof The proof is by induction on n. For
![]() $n=1$
, the theorem is the content of Theorem 1.1. Assuming that Theorem 4.1 is proved for
$n=1$
, the theorem is the content of Theorem 1.1. Assuming that Theorem 4.1 is proved for
![]() $n-1$
with
$n-1$
with
![]() $n>1$
, let us prove it for n. To this end, we set
$n>1$
, let us prove it for n. To this end, we set
![]() $P':=P_1\times \cdots \times P_{n-1}$
and
$P':=P_1\times \cdots \times P_{n-1}$
and
![]() $L'=(L_1,\dots , L_{n-1})$
.
$L'=(L_1,\dots , L_{n-1})$
.
Lemma 4.2
![]() $\mathcal O(\bar P,X)$
is isometrically isomorphic to
$\mathcal O(\bar P,X)$
is isometrically isomorphic to
![]() $\mathcal O(\bar P', \mathcal O(\bar P_n,X))$
.
$\mathcal O(\bar P', \mathcal O(\bar P_n,X))$
.
Proof We prove that the correspondence
![]() $f\mapsto f'$
,
$f\mapsto f'$
,
![]() $f\in \mathcal O(\bar P,X)$
, where
$f\in \mathcal O(\bar P,X)$
, where
gives the required isometry.
Indeed, it is clear that
![]() $f'\in C(\bar P',C(\bar P,X))$
. Next, given
$f'\in C(\bar P',C(\bar P,X))$
. Next, given
![]() $x':=(x_1,\dots ,x_{n-1})\in \bar P'$
, let us take a net
$x':=(x_1,\dots ,x_{n-1})\in \bar P'$
, let us take a net
![]() $(z^{\prime }_\alpha )\subset \mathbb D^{n-1}$
such that the net
$(z^{\prime }_\alpha )\subset \mathbb D^{n-1}$
such that the net
![]() $(L'(z^{\prime }_\alpha ))\subset P'$
converges to
$(L'(z^{\prime }_\alpha ))\subset P'$
converges to
![]() $x'$
. By the definition, each
$x'$
. By the definition, each
![]() $(f'(L'(z^{\prime }_\alpha )))\circ L_n=f(L'(z^{\prime }_\alpha ), L_n(\cdot ))$
is an X-valued holomorphic function on
$(f'(L'(z^{\prime }_\alpha )))\circ L_n=f(L'(z^{\prime }_\alpha ), L_n(\cdot ))$
is an X-valued holomorphic function on
![]() $\mathbb D$
and
$\mathbb D$
and
 $$\begin{align*}\lim_\alpha f'(L'(z^{\prime}_\alpha))(L_n(z))=\lim_\alpha f(L'(z^{\prime}_\alpha),L_n(z))=f(x',L_n(z))\\ =f'(x')(L_n(z)),\quad z\in\mathbb D. \end{align*}$$
$$\begin{align*}\lim_\alpha f'(L'(z^{\prime}_\alpha))(L_n(z))=\lim_\alpha f(L'(z^{\prime}_\alpha),L_n(z))=f(x',L_n(z))\\ =f'(x')(L_n(z)),\quad z\in\mathbb D. \end{align*}$$
Moreover, images of functions
![]() $f'(L'(z^{\prime }_\alpha ))\circ L_n\in H^\infty (\mathbb D,X)$
belong to the compact set
$f'(L'(z^{\prime }_\alpha ))\circ L_n\in H^\infty (\mathbb D,X)$
belong to the compact set
![]() $f(\bar P)\subset X$
. Thus, using a standard normal family argument for bounded holomorphic functions, we obtain that the net
$f(\bar P)\subset X$
. Thus, using a standard normal family argument for bounded holomorphic functions, we obtain that the net
![]() $(f'(L'(z^{\prime }_\alpha ))\circ L_{n})$
has a subnet converging uniformly on compact subsets of
$(f'(L'(z^{\prime }_\alpha ))\circ L_{n})$
has a subnet converging uniformly on compact subsets of
![]() $\mathbb D$
to
$\mathbb D$
to
![]() $(f'(x'))\circ L_n$
. Hence,
$(f'(x'))\circ L_n$
. Hence,
![]() $(f'(x'))\circ L_n\in H^\infty (\mathbb D,X)$
. This shows that
$(f'(x'))\circ L_n\in H^\infty (\mathbb D,X)$
. This shows that
![]() $f'\in C(\bar P',\mathcal O(\bar P_n,X)))$
.
$f'\in C(\bar P',\mathcal O(\bar P_n,X)))$
.
Similarly, given
![]() $x_n\in \bar P_n$
, one shows that
$x_n\in \bar P_n$
, one shows that
![]() $(f'\circ L')(x_n)\in H^\infty (\mathbb D^{n-1},X)$
and its image belongs to the compact set
$(f'\circ L')(x_n)\in H^\infty (\mathbb D^{n-1},X)$
and its image belongs to the compact set
![]() $f(\bar P)$
. Using the Bochner integral, we define
$f(\bar P)$
. Using the Bochner integral, we define
here,
![]() $\mathbb T_r^{n-1}$
is the boundary torus of the open polydisk
$\mathbb T_r^{n-1}$
is the boundary torus of the open polydisk
![]() $\mathbb D_r^{n-1}$
, where
$\mathbb D_r^{n-1}$
, where
![]() $\mathbb {D}_r:=\{z\in {\mathbb C}\, :\, |z|<r\}$
,
$\mathbb {D}_r:=\{z\in {\mathbb C}\, :\, |z|<r\}$
,
![]() $r\in (0,1)$
, and
$r\in (0,1)$
, and
![]() $(z_1,\dots , z_{n-1})\in \mathbb D_r^{n-1}$
. Then
$(z_1,\dots , z_{n-1})\in \mathbb D_r^{n-1}$
. Then
![]() $K_r(f'\circ L')$
is a holomorphic function on
$K_r(f'\circ L')$
is a holomorphic function on
![]() $\mathbb D_r^{n-1}$
with values in
$\mathbb D_r^{n-1}$
with values in
![]() $\mathcal O(\bar P_n,X)$
such that for each
$\mathcal O(\bar P_n,X)$
such that for each
![]() $x_n\in \bar P_n$
,
$x_n\in \bar P_n$
,
Thus,
![]() $K_r(f'\circ L')=f'\circ L'|_{\mathbb D_r^{n-1}}$
for all
$K_r(f'\circ L')=f'\circ L'|_{\mathbb D_r^{n-1}}$
for all
![]() $r\in (0,1)$
. This shows that
$r\in (0,1)$
. This shows that
![]() $f'\circ L'\in H^\infty (\mathbb D^{n-1},X)$
; hence, the correspondence
$f'\circ L'\in H^\infty (\mathbb D^{n-1},X)$
; hence, the correspondence
![]() $f\mapsto f'$
determines an isometrical isomorphism between
$f\mapsto f'$
determines an isometrical isomorphism between
![]() $\mathcal O(\bar P,X)$
and
$\mathcal O(\bar P,X)$
and
![]() $\mathcal O(\bar P', \mathcal O(\bar P_n,X))$
, as required.
$\mathcal O(\bar P', \mathcal O(\bar P_n,X))$
, as required.
Using the lemma, let us continue the proof of the theorem. To this end, let
![]() $f\in \mathcal O(\bar P,X)$
and
$f\in \mathcal O(\bar P,X)$
and
![]() $f'\in \mathcal O(\bar P',\mathcal O(\bar P_n,X))$
be as in Lemma 4.2. Then, by the induction hypothesis, there is an
$f'\in \mathcal O(\bar P',\mathcal O(\bar P_n,X))$
be as in Lemma 4.2. Then, by the induction hypothesis, there is an
![]() $F'\in \mathcal O(\mathfrak M^{n-1},\mathcal O(\bar P_n,X))$
such that
$F'\in \mathcal O(\mathfrak M^{n-1},\mathcal O(\bar P_n,X))$
such that
We define
As in Lemma 4.2, one proves that
![]() $g'\in \mathcal O(\bar P_{n},\mathcal O(\mathfrak M^{n-1},X))$
. Applying Theorem 1.1 to
$g'\in \mathcal O(\bar P_{n},\mathcal O(\mathfrak M^{n-1},X))$
. Applying Theorem 1.1 to
![]() $g'$
, we construct a function
$g'$
, we construct a function
![]() $G'\in \mathcal O(\mathfrak M,\mathcal O(\mathfrak M^{n-1},X))$
such that
$G'\in \mathcal O(\mathfrak M,\mathcal O(\mathfrak M^{n-1},X))$
such that
We set
Then F satisfies the required conditions.
Acknowledgments
I thank the anonymous referee for many helpful comments that improved the presentation of the paper.