Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T06:28:52.056Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Dual König Property of the Order-interval Hypergraph of Two Classes of N-free Posets

Published online by Cambridge University Press:  20 November 2018

Isma Bouchemakh  and
Kaci Fatma
Isma Bouchemakh
Affiliation:
L’IFORCE Laboratory, University of Sciences and Technology Houari Boumediene, Faculty of Mathematics, B.P. hz El-Alia, Bab-Ezzouar, 16111, Algiers, Algeria e-mail: [email protected]
Kaci Fatma
Affiliation:
L’IFORCE Laboratory, Mohamed Khider University of Biskra, Department of Mathematics, 07000, Algeria e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $P$ be a finite 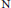$\text{N}$-free poset. We consider the hypergraph 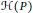$H\left( P \right)$ whose vertices are the elements of $P$ and whose edges are the maximal intervals of $P$. We study the dual König property of 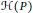$H\left( P \right)$ in two subclasses of 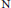$\text{N}$-free class.

Keywords

05C65posetintervalN-freehypergraphKönig propertydual König property
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 1 , 01 March 2017 , pp. 43 - 53
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Bayoumi, B. I., El-Zahar, M. H., and Khamis, S.M., Asymptotic enumeration of N-free partial orders. Order 6(1989), no. 3, 219–232. http://dx.doi.Org/10.1 OO7/BFOO563522 Google Scholar
[2] Bouchemakh, I., On the chromatic number of order-interval hypergraphs. Rostock. Math. Kolloq. 54(2000), 81–89.Google Scholar
[3] Bouchemakh, I., On the Kônig and dual Kônig properties of the order interval hypergraphs of series-parallel posets. Rostock. Math. Kolloq. 56(2002), 3-8.Google Scholar
[4] Bouchemakh, I., On the dual Kônig property of the order-interval hypergraph of a new class of posets. Rostock. Math. Kolloq. 59(2005), 19–27.Google Scholar
[5] Bouchemakh, I. and Engel, K., Interval stability and interval covering property in finite posets. Order 9(1992), no. 2, 163–175. http://dx.doi.Org/10.1007/BF00814408 Google Scholar
[6] Bouchemakh, I. and Engel, K., The order-interval hypergraph of a finite poset and the Kônig property. Discrete Math. 170(1997), 51–61. http://dx.doi.Org/10.1016/0012-365X(95)OO356-2 Google Scholar
[7] Bouchemakh, I. and Ouatiki, S., On the domatic and the total domatic numbers of the 2-section graph of the order-interval hypergraph of the finite poset. Discrete Math. 309(2009), no. 11, 3694–3679.Google Scholar
[8] Engel, K., Interval packing and covering in the Boolean lattice. Combin Probab. Comput. 5(1996), no. 4, 373–384. http://dx.doi.Org/10.1017/S0963548300002121 Google Scholar
[9] Grillet, P.A., Maximal chains and antichains. Fund. Math. 65(1969), 157–167.Google Scholar
[10] Habib, M. and Jegou, R., N-free posets as generalizations of series-parallel posets. Discrete Appl. Math. 12(1985), no. 3, 279–291. http://dx.doi.Org/10.1016/0166-21 8X(85)90030-7 Google Scholar
[11] Heuchenne, C., Sur une certaine correspondance entre graphes. Bull. Soc. Roy. Sci. Liège 33(1964), 743–753.Google Scholar
[12] Summer, D. P., Graphs indecomposable with respect to theX-join. Discrete Math. 6(1973), 281–298. http://dx.doi.Org/10.101 6/0012-365X(73)90100-3 Google Scholar
[13] Valdes, J., R. E Tarjan, and E. L Lawler, The recognition of series-parallel digraphs. Siam J. Comput. 11(1982), no. 2, 298–313. http://dx.doi.Org/!0.1137/0211023 Google Scholar