Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T01:01:47.652Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Distribution of the Sequence {nd*(n)}

Published online by Cambridge University Press:  20 November 2018

H. L. Abbott  and
M. V. Subbarao
H. L. Abbott
Affiliation:
Department of Mathematics, University of Alberta, Edmonton, Canada, T6G 2G1
M. V. Subbarao
Affiliation:
Department of Mathematics, University of Alberta, Edmonton, Canada, T6G 2G1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let d*(n) denote the number of unitary divisors of the positive integer n. For x > 1, let B(x) denote the number of integers n for which nd*(n) ≦ x. Balasubramanian and Ramachandra proved that there exists a positive constant β such that 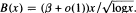. In this note we give an explicit expression for β as an infinite product, namely 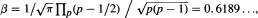where the product is over all primes p.

Keywords

10A30
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 32 , Issue 1 , 01 March 1989 , pp. 105 - 108
Copyright
Copyright © Canadian Mathematical Society 1989

References

1. Balasubramanian, R. and K. Ramachandra, On the number of integers n such that nd(n) ≦ x. Acta Arithmetica. 49 (1988), pp. 313–322. Google Scholar
2. Sathe, L., On a problem of Hardy on the distribution of integers having a given number of prime factors, J. Indian Math. Soc. 17 (1953), pp. 63–141. Google Scholar