No CrossRef data available.
Article contents
On the Discriminants of the Powers of an Algebraic Integer
Part of:
Algebraic number theory: global fields
Diophantine approximation, transcendental number theory
Published online by Cambridge University Press: 22 May 2019
Abstract
For  $\unicode[STIX]{x1D6FC}$ an algebraic integer of any degree
$\unicode[STIX]{x1D6FC}$ an algebraic integer of any degree 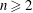 $n\geqslant 2$, it is known that the discriminants of the orders
$n\geqslant 2$, it is known that the discriminants of the orders 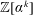 $\mathbb{Z}[\unicode[STIX]{x1D6FC}^{k}]$ go to infinity as
$\mathbb{Z}[\unicode[STIX]{x1D6FC}^{k}]$ go to infinity as 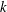 $k$ goes to infinity. We give a short proof of this result.
$k$ goes to infinity. We give a short proof of this result.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
References
Dubickas, A., On the discriminant of the power of an algebraic number. Stud. Sci. Math. Hungar. 44(2007), 27–34. https://doi.org/10.1556/SScMath.2006.1001Google Scholar
Evertse, J.-H. and Györy, K., Discriminant equations in Diophantine number theory. New Math. Monogr., 32, Cambridge University Press, Cambridge, 2017. https://doi.org/10.1017/CBO9781316160763CrossRefGoogle Scholar
Grossman, E. H., Units and discriminants of algebraic number fields. Comm. Pure Appl. Math. 27(1974), 741–747. https://doi.org/10.1002/cpa.3160270603CrossRefGoogle Scholar
Louboutin, S., On some cubic or quartic algebraic units. J. Number Theory 130(2010), 956–960. https://doi.org/10.1016/j.jnt.2009.09.002CrossRefGoogle Scholar
Louboutin, S., On the fundamental units of a totally real cubic order generated by a unit. Proc. Amer. Math. Soc. 140(2012), 429–436. https://doi.org/10.1090/S0002-9939-2011-10924-9CrossRefGoogle Scholar
Louboutin, S., Fundamental units for some orders generated by a unit. In: Publ. Math. Besançon Algèbre et Théorie des Nombres, Presses Univ. Franche-Comté, Besançon, 2015, pp. 41–68.Google Scholar



