Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-08T04:26:50.019Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Dimension of the Locus of Determinantal Hypersurfaces

Published online by Cambridge University Press:  20 November 2018

Zinovy Reichstein  and
Angelo Vistoli
Zinovy Reichstein
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC V6T 1Z2. e-mail: [email protected]
Angelo Vistoli
Affiliation:
Scuola Normale Superiore, Piazza dei Cavalieri 7, 56126 Pisa, Italy. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The characteristic polynomial 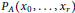${{P}_{A}}({{x}_{0}},...,{{x}_{r}})$ of an $r$-tuple 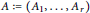$A\,:=({{A}_{1}},...,{{A}_{r}})$ of 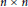$n\times n$-matrices is defined as

1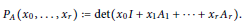

$${{P}_{A}}({{x}_{0}},...,{{x}_{r}}):=\det ({{x}_{0}}I+{{x}_{1}}{{A}_{1}}+\ldots +{{x}_{r}}{{A}_{r}}).$$

We show that if 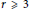$r\,\,3$ and 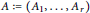$A\,:=({{A}_{1}},...,{{A}_{r}})$ is an $r$-tuple of 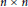$n\times n$-matrices in general position, then up to conjugacy, there are only finitely many $r$-tuples 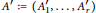$A'\,:=(A_{1}^{'},...,A_{r}^{'})$ such that 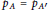${{p}_{A}}={{p}_{A'}}$. Equivalently, the locus of determinantal hypersurfaces of degree 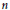$n$ in 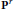${{\text{P}}^{r}}$ is irreducible of dimension 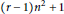$(r-1){{n}^{2}}+1$.

Keywords

14M1215A2205A10determinantal hypersurfacematrix invariantq-binomial cofficient
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 3 , 01 September 2017 , pp. 613 - 630
Copyright
Copyright © Canadian Mathematical Society 2017

References

[Beau00] Beauville, A., Determinantal hypersurfaces. Michigan Math. J. 48(2000), 39–64. http://dx.doi.Org/10.1307/mmj71030132 707 Google Scholar
[BGL14] Bermudez, H., Garibaldi, S., and Larsen, V., Linear preservers and representations with a 1-dimensional ring of invariants. Trans. Amer. Math. Soc. 366(2014), no. 9, 4755–4780. http://dx.doi.Org/10.1090/S0002-9947-2014-06081-9 Google Scholar
[CT79] Cook, R. J. and Thomas, A. D., Line bundles and homogeneous matrices. Quart. J. Math. Oxford Ser. (2) 30(1979), no. 120, 423–429. http://dx.doi.Org/10.1093/qmath/30.4.423 Google Scholar
[dCP] de Concini, C. and Procesi, C., A characteristic free approach to invariant theory, Advances in Math. 21(1976), no. 3, 330–354. http://dx.doi.Org/10.1016/S0001-8708(76)80003-5 Google Scholar
[Dieu49] Dieudonne, J., Sur une generalisation du groupe orthogonal a quatre variables. Arch. Math. 1(1949), 282–287. http://dx.doi.Org/10.1007/BF02038756 Google Scholar
[Dickson21] Dickson, L. E., Determination of all general homogeneous polynomials expressible as determinants with linear elements. Trans. Amer. Math. Soc. 22(1921), no. 2,167-179. http://dx.doi.Org/10.1090/S0002-9947-1921-1501168-0 Google Scholar
[Dolgl2] Dolgachev, I. V., Classical algebraic geometry. Cambridge University Press, Cambridge, 2012. http://dx.doi.Org/10.1017/CBO9781139084437 Google Scholar
[ES03] Eisenbud, D., Schreyer, R-O., and Weyman, J., Resultants and Chow forms via exterior syzygies. J. Amer. Math. Soc. 16(2003), no. 3, 537–579. http://dx.doi.Org/10.1090/S0894-0347-03-00423-5 Google Scholar
[FHL81] Formanek, E., Halpin, P., and Li, W. C. W., The Poincare series of the ring of 2 x 2 generic matrices. J. Algebra 69(1981), no. 1,105-112. http://dx.doi.Org/!0.1016/0021-8693(81)90130-7 Google Scholar
[FGG97] Freedman, A., Gupta, R. N., and Guralnick, R. M., Shirshov's theorem and representations of semigroups. Pacific J. Math. 1997, Special Issue, 159–176. http://dx.doi.Org/10.21 40/pjm.1 997.1 81.1 59 Google Scholar
[F1897] Frobenius, G., Uber die Darstellung der endlichen Gruppen durch lineare Substitutionen. Berlin Sitzungsber, 1897, 994–1015. Google Scholar
[G1855] Grassmann, H., Die stereometrischen Gleichungen dritten Grades, und die dadurch erzeugten Oberflachen. J. Reine Angew. Math. 49(1855), 47–65. http://dx.doi.Org/10.1515/crll.1855.49.47 Google Scholar
[H71] Herstein, I. N., Notes from a ring theory conference. Conference Board of the Mathematical Sciences Regional Conference Series in Mathematics, 9, American Mathematical Society, Providence, RI, 1971. Google Scholar
[HMS04] Holtz, O., Mehrmann, V., and Schneider, H., Potter, Wielandt, and Drazin on the matrix equation AB = coBA: new answers to old questions. Amer. Math. Monthly 111(2004), no. 8, 655–667. http://dx.doi.Org/10.2307/4145039 Google Scholar
[MM59] Marcus, M. and Moyls, B. N., Linear transformations on algebras of matrices. Canad. J. Math. 11(1959), 61–66. http://dx.doi.Org/10.4153/CJM-1959-008-0 Google Scholar
[Nell] Neretin, Yu. A., Spectral data for a pair of matrices of order 3 and the action of the group GL(2, Z). (Russian), Izv. Ross. Akad. Nauk Ser. Mat. 75(2011), no. 5, 93–102; translation in Izv.Math. 75(2011), no. 5, 959-969. http://dx.doi.Org/10.4213/im4127 Google Scholar
[P67] Procesi, C., Non-commutative affine rings. Atti Accad. Naz. Lincei Mem. Cl. Sci. Fis. Mat. Natur. Sez. I (8) 8(1967), 237–255.Google Scholar
[R93] Reichstein, Z., On automorphisms of matrix invariants induced from the trace ring. Linear Algebra Appl. 193(1993), 51–74. http://dx.doi.Org/1 0.101 6/0024-3795(93)90271-O Google Scholar
[Sch53] Schiitzenberger, M. P., Une interpretation de certaines solutions de I'equation fonctionnelle: F(x + y) = F(x)F(y). C. R. Acad. Sci. Paris 236(1953), 352–353.Google Scholar
[Vin86] Vinnikov, V., Determinantal representations of algebraic curves. In: Linear algebra in signals, systems, and control (Boston, MA, 1986), SIAM, Philadelphia, PA, pp. 73–99. Google Scholar
[Wat87] Waterhouse, W. C., Automorphisms ofdet(Xjj): the group scheme approach. Adv. in Math. 65(1987), no. 2, 171–203. http://dx.doi.Org/10.1016/0001-8708(87)90021-1 Google Scholar