Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T19:06:35.311Z Has data issue: false hasContentIssue false
  • English
  • Français

On the degree of repeated radical extensions

Part of: General field theory Field extensions

Published online by Cambridge University Press:  23 November 2020

Fernando Szechtman
Fernando Szechtman*
Affiliation:
Department of Mathematics and Statistics, University of Regina, Regina, SK, Canada
*
e-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We answer a question posed by Mordell in 1953, in the case of repeated radical extensions, and find necessary and sufficient conditions for 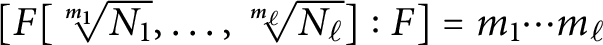$[F[\sqrt [m_1]{N_1},\dots ,\sqrt [m_\ell ]{N_\ell }]:F]=m_1\cdots m_\ell $ , where F is an arbitrary field of characteristic not dividing any 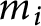$m_i$ .

Keywords

Radical extensionGalois extensionVahlen-Capelli irreducibility criterion

MSC classification

Primary: 12F05: Algebraic extensions
Secondary: 12F10: Separable extensions, Galois theory 12E05: Polynomials (irreducibility, etc.)
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 4 , December 2021 , pp. 877 - 885
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This paper is dedicated to Natalio H. Guersenzvaig. This research was partially supported by an NSERC grant.

References

Albu, T., Kummer extensions with few roots of unity . J. Number Theory 41(1992), 322–358. https://doi.org/10.1016/0022-314X(9)90131-8 CrossRefGoogle Scholar
Besicovitch, A. S., On the linear independence of fractional powers of integers . J. Lond. Math. Soc. 15(1940) 3–6. https://doi.org/10.1112/jlms/s1-15.1.3 CrossRefGoogle Scholar
Cagliero, L. and Szechtman, F., On the theorem of the primitive element with applications to the representation theory of associative and Lie algebras . Canad. Math. Bull. 57(2014), 735–748. https://doi.org/10.4153/CMB-2013-046-9 CrossRefGoogle Scholar
Capelli, A., Sulla riduttibilitá delle equazioni algebriche. Nota prima. Rend. Accad. Sci. Fis. Mat. Soc. Napoli 3(1897), 243–252.Google Scholar
Carr, R. and O’Sullivan, C., On the linear independence of roots . Int. J. Number Theory 5(2009), 161–171. https://doi.org/10.1142/S1793042109002018 CrossRefGoogle Scholar
Diviš, B., On the degrees of the sum and product of two algebraic elements . In: Number theory and algebra, Academic Press, New York, 1977, pp. 19–27.Google Scholar
Flanders, H., Advanced problems and solutions: Solutions 4797 . Amer. Math Monthly 67(1960), 188–189.Google Scholar
Hasse, H., Klasssenkörpertheorie . Mimeographed lectures, Marburg, 1932–33, pp. 187–195.Google Scholar
Isaacs, I. M., Degrees of sums in a separable field extension . Proc. Amer. Math. Soc. 25(1970), 638–641. https://doi.org/10.2307/2036661 CrossRefGoogle Scholar
Mordell, L. J., On the linear independence of algebraic numbers . Pacific J. Math. 3(1953), 625–630.CrossRefGoogle Scholar
Rédei, L., Algebra , Vol. 1. Pergamon Press, Oxford, 1967.Google Scholar
Richards, I., An application of Galois theory to elementary arithmetic . Adv. in Math. 13(1974) 268–273. https://doi.org/10.1016/0001-8708(74)90070-X CrossRefGoogle Scholar
Roth, R. L., On extension of $\mathbb{Q}$ by square roots. Amer. Math Monthly 78(1971), 392–393. https://doi.org/10.2307/2316910 CrossRefGoogle Scholar
Siegel, C. L., Algebraische Abhängigkeit von Wurzein . Acta Arith. 21(1972), 59–64. https://doi.org/10.4064/aa-21-1-59-64 CrossRefGoogle Scholar
Ursell, H. D., The degree of radical extensions . Canad. Math. Bull. 17(1974), 615–617. https://doi.org/10.4153/CMB-1974-114-x CrossRefGoogle Scholar
Vahlen, K. T., Über reductible Binome . Acta Math. 19(1895), 195–198. https://doi.org/10.1007/BF02402875 CrossRefGoogle Scholar
Vinogradov, I. M., Elements of number theory . Dover, New York, 2016.Google Scholar
Zhou, J.-P., On the degree of extensions generated by finitely many algebraic numbers . J. Number Theory 34(1990), 133–141. https://doi.org/10.1016/0022-314X(90)90144-G Google Scholar