Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-24T02:03:22.606Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Composition of Differentiable Functions

Published online by Cambridge University Press:  20 November 2018

M. Bachir  and
G. Lancien
M. Bachir
Affiliation:
Laboratoire de Mathématiques Université de Bordeaux I 351 cours de la Libération 33405 Talence cedex France, e-mail: [email protected]
G. Lancien
Affiliation:
Equipe de Mathématiques—UMR 6623 Université de Franche-Comté 25030 Besançon cedex France, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that a Banach space 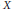$X$ has the Schur property if and only if every 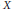$X$-valued weakly differentiable function is Fréchet differentiable. We give a general result on the Fréchet differentiability of 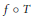$f\,\circ \,T$, where 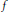$f$ is a Lipschitz function and 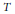$T$ is a compact linear operator. Finally we study, using in particular a smooth variational principle, the differentiability of the semi norm 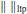${{\left\| {} \right\|}_{\text{lip}}}$ on various spaces of Lipschitz functions.

Keywords

58C2046B20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 4 , 01 December 2003 , pp. 481 - 494
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Bachir, M., A non convex analogue to Fenchel duality. J. Funct. Anal. 181 (2001), 300–312.Google Scholar
[2] Benyamini, Y. and Lindenstrauss, J., Geometric Nonlinear Functional Analysis, Vol 1. Amer.Math. Soc., Colloquium Publications, 48.Google Scholar
[3] Bourbaki, N., Eléments de Mathématique. Fasc. XXXIII, Vari étés différentielles et analytiques, Fascicule de résultats, Actualités Sci. Indust. 1333, Hermann, Paris, 1971.Google Scholar
[4] Bourgain, J. and Rosenthal, H. P., Martingales valued in certain subspaces of L1. Israel J. Math. 37 (1980), 54–75.Google Scholar
[5] Deville, R., Godefroy, G. and Zizler, V., A smooth variational principle with applications to Hamilton-Jacobi equations in infinite dimensions. J. Funct. Anal. 111 (1993), 197–212.Google Scholar
[6] Ghoussoub, N., Duality and Perturbation Methods in Critical Point Theory. Cambridge Tracts in Math. 64, Cambridge University Press.Google Scholar
[7] Gutiérrez, J. M. and Llavona, J. G., Composition operators between algebras of differentiable functions. Trans. Amer.Math. Soc. 338 (1993), 769–782.Google Scholar
[8] Handbook of the Geometry of Banach spaces, Vol. 1. (eds., Johnson and Lindenstrauss), North Holland, 2001.Google Scholar