Published online by Cambridge University Press: 16 December 2019
In this note we prove that the Kalton interlaced graphs do not equi-coarsely embed into the James space 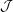 ${\mathcal{J}}$ nor into its dual
${\mathcal{J}}$ nor into its dual 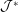 ${\mathcal{J}}^{\ast }$. It is a particular case of a more general result on the non-equi-coarse embeddability of the Kalton graphs into quasi-reflexive spaces with a special asymptotic structure. This allows us to exhibit a coarse invariant for Banach spaces, namely the non-equi-coarse embeddability of this family of graphs, which is very close to but different from the celebrated property
${\mathcal{J}}^{\ast }$. It is a particular case of a more general result on the non-equi-coarse embeddability of the Kalton graphs into quasi-reflexive spaces with a special asymptotic structure. This allows us to exhibit a coarse invariant for Banach spaces, namely the non-equi-coarse embeddability of this family of graphs, which is very close to but different from the celebrated property 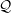 ${\mathcal{Q}}$ of Kalton. We conclude with a remark on the coarse geometry of the James tree space
${\mathcal{Q}}$ of Kalton. We conclude with a remark on the coarse geometry of the James tree space 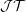 ${\mathcal{J}}{\mathcal{T}}$ and of its predual.
${\mathcal{J}}{\mathcal{T}}$ and of its predual.
The first and third named authors are supported by the French “Investissements d’Avenir” program, project ISITE-BFC (contract ANR-15-IDEX-03).