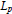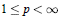Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Giner, Emmanuel
2009.
Calmness Properties and Contingent Subgradients of Integral Functionals on Lebesgue Spaces L p , 1 ≼ p < ∞.
Set-Valued and Variational Analysis,
Vol. 17,
Issue. 3,
p.
223.
Chieu, Nguyen Huy
2010.
Integral of the Clarke subdifferential mapping and a generalized Newton–Leibniz formula.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 73,
Issue. 3,
p.
614.
Penot, Jean-Paul
2011.
Image space approach and subdifferentials of integral functionals.
Optimization,
Vol. 60,
Issue. 1-2,
p.
69.
Penot, Jean-Paul
2013.
Calculus Without Derivatives.
Vol. 266,
Issue. ,
p.
407.
Penot, Jean-Paul
2013.
Calculus Without Derivatives.
Vol. 266,
Issue. ,
p.
463.
Penot, Jean-Paul
2013.
Calculus Without Derivatives.
Vol. 266,
Issue. ,
p.
357.
Penot, Jean-Paul
2013.
Calculus Without Derivatives.
Vol. 266,
Issue. ,
p.
187.
Penot, Jean-Paul
2013.
Calculus Without Derivatives.
Vol. 266,
Issue. ,
p.
263.
Penot, Jean-Paul
2013.
Calculus Without Derivatives.
Vol. 266,
Issue. ,
p.
117.
Giner, Emmanuel
and
Penot, Jean-Paul
2018.
Subdifferentiation of integral functionals.
Mathematical Programming,
Vol. 168,
Issue. 1-2,
p.
401.
Correa, Rafael
Hantoute, Abderrahim
and
Pérez-Aros, Pedro
2020.
Subdifferential Calculus Rules for Possibly Nonconvex Integral Functions.
SIAM Journal on Control and Optimization,
Vol. 58,
Issue. 1,
p.
462.
Garrido, Juan Guillermo
Pérez-Aros, Pedro
and
Vilches, Emilio
2023.
Random Multifunctions as Set Minimizers of Infinitely Many Differentiable Random Functions.
Journal of Optimization Theory and Applications,
Vol. 198,
Issue. 1,
p.
86.
Fumagalli, Alessio
and
Patacchini, Francesco Saverio
2023.
Well-posedness and variational numerical scheme for an adaptive model in highly heterogeneous porous media.
Journal of Computational Physics,
Vol. 475,
Issue. ,
p.
111844.