Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T15:46:55.104Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Cardinality of Urysohn Spaces

Published online by Cambridge University Press:  20 November 2018

A. Bella  and
F. Cammaroto
A. Bella
Affiliation:
Department of Mathematics, University of Messina98010 -, Messina, Italy
F. Cammaroto
Affiliation:
Department of Mathematics, University of Messina98010 -, Messina, Italy
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper some cardinal inequalities for Urysohn spaces are established. In particular the following two theorems are proved:

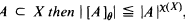(i)If where [A]θ denotes the θ-closed hull of A, i.e., the smallest θ-closed subset of X containing A;

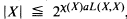(ii), where aL(X, X) is the smallest cardinal number m such that for every open cover 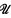of X there is a subfamily 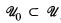for which

Keywords

Cardinal functionsθ-closed setsalmost Lindelöf degreePrimary54A25Secondary54D20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 31 , Issue 2 , 01 June 1988 , pp. 153 - 158
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Arkhangel'skii, A., The power of bicompacta with the first axiom of countability, Dokl. Akad. Nauk S.S.S.R. 187 (1969), pp. 967–970. (Soviet Math. Dokl. 10 (1969), pp. 951-955).Google Scholar
2. Dikranjan, D. and Giuli, E., S(n)-θ-Closed spaces, Topology Appl., to appear.Google Scholar
3. Engelking, R., General topology, (Monografie Matematyczne, Warszawa 1977).Google Scholar
4. Juhasz, I., Cardinal functions in topology, Math. Centre Tracts 34, Amsterdam (1971).Google Scholar
5. Pol, R., Short proofs of two theorems on cardinality of topological spaces, Bull. Acad. Polon. Sci. Ser. Math. Astr. Phys. 22 (1974), pp. 1245–1249.Google Scholar
6. Veličko, N., H-closed topological spaces, Mat. Sb. (N.S.) 70 (112) (1966), pp. 98–112; Amer. Math. Soc. Transi. 78 (Ser. 2) (1969), pp. 103-118.Google Scholar
7. Viglino, G., C-compact spaces, Duke Math. J. 36 (1969), pp. 761–764.Google Scholar
8. Willard, S. and Dissanayake, B., The almost-Lindelôf degree, Canad. Math. Bull. 27 (4) (1984), pp. 1–4.Google Scholar