Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-05T04:55:39.247Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Branch Points in the Branched Coverings of Links

Published online by Cambridge University Press:  20 November 2018

Shintchi Kinoshita
Shintchi Kinoshita*
Affiliation:
Deparment of mathematics and computer science, Florida state universityTallahassee, florida 32306
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let l be a polygonal link in a 3-sphere S3 and 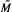a branched covering of l, which depends on the choice of a monodromy map ϕ. Let be the link in 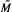over l. In this paper we determine the exact position of in 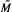for some cases. For instance, if l is a torus link ((n + 1)p, n) and ϕ is an appropriate monodromy map of the fundamental group of S3 - l into the symmetric group of degree n + 1, then 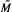is an S3 and l is a torus link (np,n2). The 3-fold irregular branched covering of a doubled knot k is an S3, if it exists. The position of the link over k is shown in a figure. The link over knot 61 is obtained by K. A. Perko and the author, independently, and shown without proof in a paper by R. H. Fox [Can. J. Math. 22 (1970), 193-201]. The result mentioned in the above includes this case.

Keywords

57M2557M12
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 28 , Issue 2 , 01 June 1985 , pp. 165 - 173
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Burde, G., On branched coverings of S3 Can. J. Math., 23 (1971), 84–89.Google Scholar
2. FOX, R.H., Covering spaces with singularities, Algebraic geometry and topology. A symposium in honor of S. Lefschetz. Princeton Univ. Press, Princeton, N.J., 1957, 234–257.Google Scholar
3. FOX, R.H. A quick trip through knot theory, Topology of 3-manifolds and related topics. Proc. The Univ. of Georgia Institute. 1961. Prentice-Hall, Englewood Cliffs, N.J., 1962, 213–216.Google Scholar
4. FOX, R.H. Construction of simply connected 3-manifolds, loc. cit.Google Scholar
5. FOX, R.H. Metacyclic invariants of knots and links. Can. J. Math. 22 (1970), 193–201.Google Scholar
6. Gordon, C. McA and Heil, W., Simply-connected branched coverings of S3. Proc. Amer. Math. Soc. 35 (1972), 287-288.Google Scholar
7. Neuwirth, L.P., Knot groups. Princeton Univ. Press, Princeton, N.J., 1965.Google Scholar
8. Rolfson, D., Knots and links. Publish or Perish Inc., Berkeley, Calif., 1976.Google Scholar
9. Seifert, H. and Threlfall, W., Lehrbuch der Topologie. Teubner, Leipzig and Berlin, 1934.Google Scholar