Hostname: page-component-f554764f5-wjqwx Total loading time: 0 Render date: 2025-04-08T16:33:56.561Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Boundary and Tensor Product of Function Algebras

Published online by Cambridge University Press:  20 November 2018

A. S. Fox
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 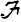be an arbitrary family of continuous complex-valued functions defined on a compact Hausdorff space X. A closed subset B ⊆ X is called a boundary for 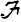if every 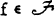attains its maximum modulus at some point of B. A boundary, B, is said to be minimal if there exists no boundary for 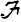properly contained in B. It can be shown that minimal boundaries exist regardless of the algebraic structure which 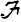may possess. Under certain conditions on the family 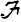, it can be shown that a unique minimal boundary for 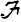exists. In particular, this is the case if 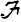is a subalgebra or subspace of C(X) where X is compact and Hausdorff (see for example [2]). This unique minimal boundary for an algebra 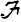of functions is called the Silov boundary of .

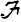Type
Notes and Problems
Information
Canadian Mathematical Bulletin , Volume 9 , Issue 1 , April 1966 , pp. 103 - 106
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Arens, R. and Singer, I. M., Function Values as Boundary Integrals, Proc. Amer. Math. Soc., Vol. 5, 1954, pp. 735-745.Google Scholar
2. Bear, H. S., The śilov Boundary for a Linear Space of Continuous Functions, Amer. Math. Monthly, May 1961, pp. 483.Google Scholar
3. Naimark, M.A., Normed Rings, Noordhoff, 1959, pp.212 et seq.Google Scholar
4. Rickart, C. E., The General Theory of Banach Algebras, Van Nostrand, 1960.Google Scholar