Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-31T19:31:46.428Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Bernstein Problem in the Three-dimensional Heisenberg Group

Published online by Cambridge University Press:  20 November 2018

Josef F. Dorfmeister ,
Jun-ichi Inoguchi  and
Shimpei Kobayashi
Josef F. Dorfmeister
Affiliation:
Fakultät für Mathematik, TU-München, Boltzmann str. 3, D-85747, Garching, Germany e-mail: [email protected]
Jun-ichi Inoguchi
Affiliation:
Institute of Mathematics, University of Tsukuba, Tsukuba 305-8571, Japan e-mail: [email protected]
Shimpei Kobayashi
Affiliation:
Department of Mathematics, Hokkaido University, Sapporo, 060-0810, Japan e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we present a simple alternative proof for the Bernstein problem in the three dimensional Heisenberg group 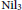$\text{Ni}{{\text{l}}_{3}}$ by using the loop group technique. We clarify the geometric meaning of the two-parameter ambiguity of entire minimal graphs with prescribed Abresch-Rosenberg differential.

Keywords

53A1053C42Bernstein problemminimal graphsHeisenberg grouploop groupsspinors
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 1 , 01 March 2016 , pp. 50 - 61
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Abresch, U. and Rosenberg, H.. Generalized Hopf differentials. Mat. Contemp. 28(2005), 1–28.Google Scholar
[2] Brander, D., Rossman, W.. and Schmitt, N.. Holomorphic representation of constant mean curvature surfaces in Minkowski space: consequences of non-compactness in loop group methods. Adv. in Math. 223(2010), 949–986. http://dx.doi.Org/10.1016/j.aim.2009.09.006 Google Scholar
[3] Cheng, S-Y. and Yau, S-T., Maximal space-like hypersurfaces in the Lorentz-Minkowski spaces. Ann. Math. (2) 104(1976), no. 3, 407–419. http://dx.doi.Org/10.2307/1 970963 Google Scholar
[4] E. Dorfmeister, J., Inoguchi, J.. and Kobayashi, S.-P., A loop group method for minimal surfaces in the three-dimensional Heisenberg group. Asian J. Math., to appear. arxiv:1210.7300v3Google Scholar
[5] Inoguchi, J., Kumamoto, T.. Ohsugi, N.. and Suyama, Y.. Differential geometry of curves and surfaces in 3-dimensional homogeneous spaces I, II. Fukuoka Univ. Sci. Rep. 29(2000), 155–182; 30(2000), 17-47.Google Scholar
[6] Fernandez, I. and Mira, P.. Holomorphic quadratic differentials and the Bernstein problem in Heisenberg space. Trans. Amer. Math. Soc. 361(2009), no. 11, 5737–5752. http://dx.doi.Org/10.1090/S0002-9947-09-04645-5 Google Scholar
[7] Milnor, T. K., A conformai analog of Bernstein's theorem in Minkowski 3-space. In: The legacy of Sonya Kovalevskaya, Contemp. Math., 64, American Mathematical Society, Providence, RI, 1987, pp. 123–132. Google Scholar
[8] Thurston, W. M., Three-dimensional geometry and topology, Vol. 1. Princeton Mathematical Series, 35, Princeton University Press, Princeton, NJ, 1997.Google Scholar
[9] Wan, T. Y.-H., Constant mean curvature surface, harmonic maps, and universal Teichmuller space. J. Differential Geom. 35(1992), no. 3, 643–657.Google Scholar
[10] Wan, T. Y.-H. and Au, T. K.-K., Parabolic constant mean curvature spacelike surfaces. Proc. Amer. Math. Soc. 120(1994), no. 2,559-564, http://dx.doi.Org/10.1090/S0002-9939-1994-1169052-5 Google Scholar