No CrossRef data available.
Article contents
On the Absolute Nörlund Summability of a Fourier Series
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 
be a given infinite series and {sn} the sequence of its partial sums. Let {pn} be a sequence of constants, real or complex, and let us write
(1.1)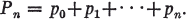
If
(1.2)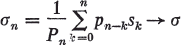
as n→∞, we say that the series 
is summable by the Nörlund method (N,pn) to σ. The series is said to be absolutely summable (N,pn) or summable |N,pn| if σn is of bounded variation, i.e.,
(1.3)
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1973
References
1.
Alexits, G., Convergence problems of orthogonal series, Pergamon Press, New York, 1961.Google Scholar
2.
Bhatt, S. N., An aspect of the local property of |N, pn| summability of a Fourier series, Indian J. Math.
5 (1963), 87–91.Google Scholar
3.
Hsiang, F. C., On the absolute Nörlund summability of a Fourier series, J. Austral. Math. Soc.
7 (1967), 252–256.Google Scholar
You have
Access