Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T01:40:17.998Z Has data issue: false hasContentIssue false
  • English
  • Français

On Super Weakly Compact Convex Sets and Representation of the Dual of the Normed Semigroup They Generate

Published online by Cambridge University Press:  20 November 2018

Lixin Cheng ,
Zhenghua Luo  and
Yu Zhou
Lixin Cheng
Affiliation:
School of Mathematical Sciences, Xiamen University, Xiamen, 361005, China e-mail: [email protected]@hotmail.com [email protected]@126.com
Zhenghua Luo
Affiliation:
School of Mathematical Sciences, Xiamen University, Xiamen, 361005, China e-mail: [email protected]@hotmail.com [email protected]@126.com
Yu Zhou
Affiliation:
School of Mathematical Sciences, Xiamen University, Xiamen, 361005, China e-mail: [email protected]@hotmail.com [email protected]@126.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

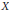In this note, we first give a characterization of super weakly compact convex sets of a Banach space $X$: a closed bounded convex set 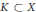$K\,\subset \,X$ is super weakly compact if and only if there exists a 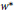${{w}^{*}}$ lower semicontinuous seminorm 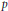$P$ with 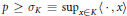$P\,\ge \,{{\sigma }_{K}}\,\equiv \,{{\sup }_{x\in K}}\left\langle \,\cdot \,,\,x \right\rangle $ such that 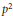${{P}^{2}}$ is uniformly Fréchet differentiable on each bounded set of 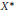${{X}^{*}}$. Then we present a representation theoremfor the dual of the semigroup swcc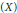$\left( X \right)$ consisting of all the nonempty super weakly compact convex sets of the space 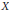$X$.

Keywords

20M3046B1046B2046E1546J1049J50super weakly compact setdual of normed semigroupuniform Fréchet differentiabilityrepresentation.
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 2 , 01 June 2013 , pp. 272 - 282
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Benyamini, Y. and Lindenstauss, J., Geometric nonlinear functional analysis. I. Colloq. Publ. 48, American Mathematical Society, 2000.Google Scholar
[2] Borwein, J. M., A note on “-subgradients and maximal monotonicity. Pacific J. Math. 103(1982), no. 2, 307–314. Google Scholar
[3] Brøndsted, A. and Rockafellar, R. T., On the subdifferentiability of convex functions. Proc. Amer. Math. Soc. 16(1965), 605–611..Google Scholar
[4] Cepedello-Boiso, M., Approximation of Lipschitz functions by Δ-convex functions in Banach spaces. Israel J. Math. 106(1998), 269–284. http://dx.doi.org/10.1007/BF02773472 Google Scholar
[5] Cheng, L., Cheng, Q., and Luo, Z., On some new characterizations of weakly compact sets in Banach spaces. Studia Math. 201(2010), no. 2, 155–166. http://dx.doi.org/10.4064/sm201-2-3 Google Scholar
[6] Cheng, L., Cheng, Q., Wang, B., and Zhang, W., On super-weakly compact sets and uniformly convexifiable sets. Studia Math. 199(2010), no. 2, 145–169. http://dx.doi.org/10.4064/sm199-2-2 Google Scholar
[7] Cheng, L. and Zhou, Y., On approximation by Δ-convex polyhedron support functions and the dual of cc(X) and wcc(X). J. Convex Anal. 19(2012), no. 1, [final page numbers not yet available].Google Scholar
[8] Deville, R., Godefroy, G., and Zizler, V., Smoothness and renormings in Banach spaces. Pitman Monographs and Surveys in Pure and Applied Mathematics, 64, Longman Scientific & Technical, Harlow; JohnWiley & Sons, Inc., New York, 1993.Google Scholar
[9] Enflo, P., Banach spaces which can be given an equivalent uniformly convex norm. Israel J. Math. 13(1972), 281–288. http://dx.doi.org/10.1007/BF02762802Google Scholar
[10] Fabian, M., Gâteaux differentiability of convex functions and topology. weak Asplund spaces. Canadian Mathematical Society Series of Monographs and Advanced Texts, JohnWiley & Sons, Inc., New York, 1997.Google Scholar
[11] Keimel, K. andRoth, W., Ordered cones and approximation. Lecture Notes in Mathematics, 1517, Springer-Verlag, Berlin, 1992.Google Scholar
[12] Phelps, R. R., Convex functions, monotone operators and differentiability. Lecture Notes in Mathematics, 1364, Springer-Verlag, Berlin, 1989.Google Scholar
[13] Piser, G., Martingales with values in uniformly convex spaces. Israel J. Math. 20(1975), no. 3–4. 326–350. http://dx.doi.org/10.1007/BF02760337 Google Scholar
[14] Radström, H., An embedding theorem for spaces of convex sets. Proc. Amer. Math. Soc. 3(1952), 165–169. http://dx.doi.org/10.2307/2032477 Google Scholar
[15] Wu, C. X. and Cheng, L. X., A note on differentiability of convex functions. Proc. Amer. Math. Soc. 121(1994), no. 4, 1057–1062. Google Scholar