Published online by Cambridge University Press: 20 November 2018
The purpose of this paper is to obtain a set of sufficient conditions for “global asymptotic stability” of the trivial solution x = 0 of the differential equation
1.1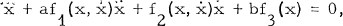
using a Lyapunov function which is substantially different from similar functions used in [2], [3] and [4], for similar differential equations. The functions f1, f2 and f3 are real - valued and are smooth enough to ensure the existence of the solutions of (1.1) on [0, ∞). The dot indicates differentiation with respect to t. We are taking a and b to be some positive parameters.