Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Roman, Steven M
and
Rota, Gian-Carlo
1978.
The umbral calculus.
Advances in Mathematics,
Vol. 27,
Issue. 2,
p.
95.
Prodinger, Helmut
1983.
Ordered Fibonacci Partitions.
Canadian Mathematical Bulletin,
Vol. 26,
Issue. 3,
p.
312.
Benoumhani, Moussa
1996.
On Whitney numbers of Dowling lattices.
Discrete Mathematics,
Vol. 159,
Issue. 1-3,
p.
13.
Benoumhani, Moussa
1997.
On Some Numbers Related to Whitney Numbers of Dowling Lattices.
Advances in Applied Mathematics,
Vol. 19,
Issue. 1,
p.
106.
Hsu, Leetsch C.
and
Shiue, Peter Jau-Shyong
1999.
On certain summation problems and generalizations of Eulerian polynomials and numbers.
Discrete Mathematics,
Vol. 204,
Issue. 1-3,
p.
237.
Liu, Lily L.
and
Wang, Yi
2007.
A unified approach to polynomial sequences with only real zeros.
Advances in Applied Mathematics,
Vol. 38,
Issue. 4,
p.
542.
Chen, William Y. C.
Wang, Larry X. W.
and
Yang, Arthur L. B.
2011.
Recurrence Relations for Strongly q-Log-Convex Polynomials.
Canadian Mathematical Bulletin,
Vol. 54,
Issue. 2,
p.
217.
Corcino, Roberto B.
Corcino, Cristina B.
and
Papaschinopoulos, Garyfalos
2011.
On Generalized Bell Polynomials.
Discrete Dynamics in Nature and Society,
Vol. 2011,
Issue. 1,
Rahmani, Mourad
2014.
Some results on Whitney numbers of Dowling lattices.
Arab Journal of Mathematical Sciences,
Vol. 20,
Issue. 1,
p.
11.
2015.
Commutation Relations, Normal Ordering, and Stirling Numbers.
p.
419.
Rahmani, Mourad
2015.
On p-Bernoulli numbers and polynomials.
Journal of Number Theory,
Vol. 157,
Issue. ,
p.
350.
Mangontarum, Mahid M.
Cauntongan, Omar I.
and
Macodi-Ringia, Amila P.
2016.
The Noncentral Version of the Whitney Numbers: A Comprehensive Study.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2016,
Issue. ,
p.
1.
Kargın, Levent
and
Corcino, Roberto B.
2016.
Generalization of Mellin derivative and its applications.
Integral Transforms and Special Functions,
Vol. 27,
Issue. 8,
p.
620.
Liu, Lily Li
and
Ma, Dan
2017.
Some polynomials related to Dowling lattices and x-Stieltjes moment sequences.
Linear Algebra and its Applications,
Vol. 533,
Issue. ,
p.
195.
Corcino, Cristina B
Corcino, Roberto B
Mező, István
and
Ramírez, José L
2018.
Some polynomials associated with the $${\varvec{r}}$$ r -Whitney numbers.
Proceedings - Mathematical Sciences,
Vol. 128,
Issue. 3,
Kargın, Levent
2018.
p-Bernoulli and geometric polynomials.
International Journal of Number Theory,
Vol. 14,
Issue. 02,
p.
595.
Kargin, Levent
and
Rahmani, Mourad
2018.
A closed formula for the generating function of p-Bernoulli numbers.
Quaestiones Mathematicae,
Vol. 41,
Issue. 7,
p.
975.
Qi, Feng
2019.
Determinantal expressions and recurrence relations for Fubini and Eulerian polynomials.
Journal of Interdisciplinary Mathematics,
Vol. 22,
Issue. 3,
p.
317.
Zhu, Bao-Xuan
2019.
Positivity and continued fractions from the binomial transformation.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 149,
Issue. 03,
p.
831.
Goubi, Mouloud
2020.
New family of special numbers associated with finite operator.
Mathematica Moravica,
Vol. 24,
Issue. 2,
p.
83.


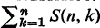 where
where 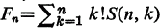 and polynomials
and polynomials 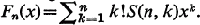 .
.