Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-29T02:26:56.674Z Has data issue: false hasContentIssue false
  • English
  • Français

On Sets of Ternary Vectors Whose Only Linear Dependencies Involve an Odd Number of Vectors

Published online by Cambridge University Press:  20 November 2018

E. R. Berlekamp
E. R. Berlekamp*
Affiliation:
Bell Telephone Laboratories, Inc., Murray Hill, New Jersey
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recent efforts to generalize a classic result of Hajos [3] on the decomposition of finite abelian groups into direct sums of subsets (see Fuchs [1, Chap. XV]) led B. Gordon [2] to the following conjecture. If are r-dimensional row vectors over GF(3) such that: (i) Any weighted (±) sum of any even number of 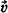's is nonzero, (ii) For each r-dimensional 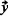, there exists an s such that

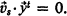
Then there exists a subset of either 1 or 4 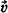's which satisfies the same conditions.

This paper proves Gordon's conjecture.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 3 , September 1970 , pp. 363 - 366
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Fuchs, L., Abelian groups, Publ. House of the Hungarian Acad, of Sci. Budapest, 1958.Google Scholar
2. Gordon, B., (unpublished communication), 1968.Google Scholar
3. Hajos, G., Über einfache und mehrfache Bedeckung des n-dimensionalen Raumes mit einem Würfelgitter, Math. Z. 47 (1942), 427-467.Google Scholar