Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kozyrev, V. P.
1974.
Graph theory.
Journal of Soviet Mathematics,
Vol. 2,
Issue. 5,
p.
489.
Barthélemy, Jean-Pierre
Hudry, Olivier
Isaak, Garth
Roberts, Fred S.
and
Tesman, Barry
1995.
The reversing number of a diagraph.
Discrete Applied Mathematics,
Vol. 60,
Issue. 1-3,
p.
39.
Darrah, Marjorie
Liu, Yi-Ping
and
Zhang, Cun-Quan
1997.
Cycles of all lengths in arc-3-cyclic semicomplete digraphs.
Discrete Mathematics,
Vol. 173,
Issue. 1-3,
p.
23.
Vandell, Robert C.
2002.
Maximum Arc-integrity of Tournaments and Bipartite Tournaments.
Electronic Notes in Discrete Mathematics,
Vol. 11,
Issue. ,
p.
612.
Kenyon-Mathieu, Claire
and
Schudy, Warren
2007.
How to rank with few errors.
p.
95.
Charon, Irène
and
Hudry, Olivier
2007.
A survey on the linear ordering problem for weighted or unweighted tournaments.
4OR,
Vol. 5,
Issue. 1,
p.
5.
Alon, Noga
Lokshtanov, Daniel
and
Saurabh, Saket
2009.
Automata, Languages and Programming.
Vol. 5555,
Issue. ,
p.
49.
Charon, Irène
and
Hudry, Olivier
2010.
An updated survey on the linear ordering problem for weighted or unweighted tournaments.
Annals of Operations Research,
Vol. 175,
Issue. 1,
p.
107.
Reid, K
2013.
Handbook of Graph Theory, Second Edition.
Vol. 20134658,
Issue. ,
p.
196.
Downey, Rodney G.
and
Fellows, Michael R.
2013.
Fundamentals of Parameterized Complexity.
p.
143.
Bollobás, Béla
and
Scott, Alex
2015.
Intersections of random hypergraphs and tournaments.
European Journal of Combinatorics,
Vol. 44,
Issue. ,
p.
125.
Ostovari, Mojtaba
and
Zarei, Alireza
2024.
A better LP rounding for feedback arc set on tournaments.
Theoretical Computer Science,
Vol. 1015,
Issue. ,
p.
114768.
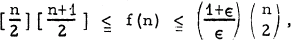 where [x] denotes the largest integer not exceeding x, and the second inequality holds for any fixed ∈ > 0 and all sufficiently large n.
where [x] denotes the largest integer not exceeding x, and the second inequality holds for any fixed ∈ > 0 and all sufficiently large n.