Article contents
On p-Large Subgroups of p-Torsion Groups
Published online by Cambridge University Press: 20 November 2018
Resumé
Les groupes p-torsion forment une classe de groupes abéliens mixtes dont les sous-groupes de p-base sont de torsion. Nous montrons ici que la généralisation naturelle à ces groupes de la notion de sous-groupe large développée pour les groupes primaires par R. S. Pierce, permet d'obtenir des résultats analogues. Ainsi nous caractérisons les sous-groupes p-larges d'un groupe p-torsion G en fonction des suites non-décroissantes d'entiers non-négatifs u = (ui) qui satisfont à la condition d'écart pour G. On obtient: un sous-groupe A du groupe p-torsion G est p-large si, et seulement si A est de la forme G(u) pour une suite u telle que pour tout x ∈ G, la suite (h(pix)) est plus grande presque partout que la suite u.
Nous déterminons aussi, les sous-groupes p-large de 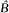 , le complété p-adique d'une somme directe de groupes cycliques non bornés B, ainsi que ceux des sous-groupes p-purs totalement invariants de
, le complété p-adique d'une somme directe de groupes cycliques non bornés B, ainsi que ceux des sous-groupes p-purs totalement invariants de 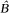 engendrés par un élément.
engendrés par un élément.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1984
Footnotes
The work of this author is partially supported by the Canadian N.S.E.R.C. grant no A5591.
References
- 1
- Cited by


