No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
We give sufficient conditions for the following problem: given a topological space 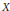 $X$, a metric space
$X$, a metric space 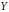 $Y$, a subspace
$Y$, a subspace 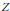 $Z$ of
$Z$ of 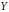 $Y$, and a continuous map
$Y$, and a continuous map 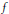 $f$ from
$f$ from 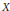 $X$ to
$X$ to 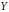 $Y$, is it possible, by applying to
$Y$, is it possible, by applying to 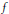 $f$ an arbitrarily small perturbation, to ensure that
$f$ an arbitrarily small perturbation, to ensure that 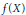 $f\left( {{X}^{'}} \right)$ does not meet
$f\left( {{X}^{'}} \right)$ does not meet 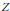 $Z$? We also give a relative variant: if
$Z$? We also give a relative variant: if 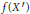 $f\left( X\prime \right)$ does not meet
$f\left( X\prime \right)$ does not meet 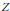 $Z$ for a certain subset
$Z$ for a certain subset 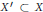 ${X}'\subset X$, then we may keep
${X}'\subset X$, then we may keep 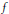 $f$ unchanged on
$f$ unchanged on 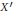 ${X}'$. We also develop a variant for continuous sections of fibrations and discuss some applications to matrix perturbation theory.
${X}'$. We also develop a variant for continuous sections of fibrations and discuss some applications to matrix perturbation theory.