Article contents
On Periodic Solutions of x‴ + ax″ + b′ + g(x) = 0
Published online by Cambridge University Press: 20 November 2018
Extract
In [1] J. O. C. Ezeilo asks whether the equation
1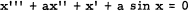
has periodic solutions for a ≠ 0. Since (1) has a two-dimensional space of solutions of period 2π if sin x is approximated by x, it is plausible to conclude, by analogy with x″ + sin x = 0, that (1) does have periodic solutions. However, when one applies the standard theory of perturbation of periodic solutions (treating a as small, see [2]), one finds that the only real periodic solutions obtainable in this manner are the trivial ones x(t, a) = nπ for some integer n.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1967
Footnotes
This research was carried out while the author was partially supported by a grant from the Canada Council.
References
- 1
- Cited by


