Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Oswald, A.
1977.
A Note on Injective Modules Over a d.g. Near-Ring.
Canadian Mathematical Bulletin,
Vol. 20,
Issue. 2,
p.
267.
Banaschewski, Bernhard
and
Nelson, Evelyn
1977.
On the Non-Existence of Injective Near-Ring Modules.
Canadian Mathematical Bulletin,
Vol. 20,
Issue. 1,
p.
17.
1977.
Near-Rings - The Theory and its Applications.
Vol. 23,
Issue. ,
p.
437.
Meldrum, John D. P.
1978.
Injective near-ring modules over 𝑍_{𝑛}.
Proceedings of the American Mathematical Society,
Vol. 68,
Issue. 1,
p.
16.


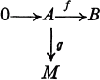 can be embedded into a commutative diagram
can be embedded into a commutative diagram 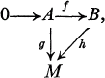 where A and B are right
where A and B are right 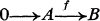 exact.
exact.