Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-15T09:57:33.007Z Has data issue: false hasContentIssue false
  • English
  • Français

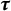On infinitesimal $\boldsymbol { \tau }$-isospectrality of locally symmetric spaces

Part of: Lie groups Global differential geometry

Published online by Cambridge University Press:  09 January 2025

Chandrasheel Bhagwat Open the ORCID record for Chandrasheel Bhagwat [Opens in a new window] ,
Kaustabh Mondal Open the ORCID record for Kaustabh Mondal [Opens in a new window]  and
Gunja Sachdeva Open the ORCID record for Gunja Sachdeva [Opens in a new window]
Chandrasheel Bhagwat*
Affiliation:
Department of Mathematics, Indian Institute of Science Education and Research, Pune, Dr. Homi Bhabha Road, Pashan, Pune, 411008, India e-mail: [email protected]
Kaustabh Mondal
Affiliation:
Department of Mathematics, Indian Institute of Science Education and Research, Pune, Dr. Homi Bhabha Road, Pashan, Pune, 411008, India e-mail: [email protected]
Gunja Sachdeva
Affiliation:
Department of Mathematics, BITS Pilani, K.K. Birla Goa Campus, Zuarinagar, Goa 403726, India e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 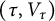$(\tau , V_{\tau })$ be a finite dimensional representation of a maximal compact subgroup K of a connected non-compact semisimple Lie group G, and let 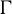$\Gamma $ be a uniform torsion-free lattice in G. We obtain an infinitesimal version of the celebrated Matsushima–Murakami formula, which relates the dimension of the space of automorphic forms associated to 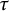$\tau $ and multiplicities of irreducible 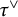$\tau ^\vee $-spherical spectra in 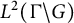$L^2(\Gamma \backslash G)$. This result gives a promising tool to study the joint spectra of all central operators on the homogenous bundle associated to the locally symmetric space and hence its infinitesimal 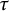$\tau $-isospectrality. Along with this, we prove that the almost equality of 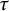$\tau $-spherical spectra of two lattices assures the equality of their 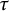$\tau $-spherical spectra.

Keywords

Representation equivalenceisospectralitySelberg trace formulanon-compact symmetric space

MSC classification

Primary: 22E40: Discrete subgroups of Lie groups 22E45: Representations of Lie and linear algebraic groups over real fields 53C35: Symmetric spaces
Type
Article
Information
Canadian Mathematical Bulletin , Volume 68 , Issue 1 , March 2025 , pp. 246 - 261
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

K. Mondal thanks Prime Minister Research Fellowship (PMRF) Govt. of India for supporting this work partially. G. Sachdeva’s research is supported by Department of Science Technology-Science and Engineering Research Board, Govt. of India POWER Grant [SPG/2022/001738].

References

Chandrasheel, B. and Rajan, C. S., On a spectral analog of the strong multiplicity one theorem . Int. Math. Res. Not. IMRN 2011(2011), no. 18, 4059–4073.Google Scholar
Chandrasheel, B., and Gunja, S., Results on a strong multiplicity one theorem . New York J. Math. 30(2024), 1556–1565.Google Scholar
Dubi, K., A refinement of strong multiplicity one for spectra of hyperbolic manifolds . Trans. Amer. Math. Soc. 366(2014), no. 11, 5925–5961.Google Scholar
Knapp, A., Representation theory of semisimple groups: An overview based on examples, Princeton University Press, New Jersey, 2001.Google Scholar
Lauret, E. A. and Miatello, R. J., Strong multiplicity one theorems for locally homogeneous spaces of compact-type . Proc. Amer. Math. Soc. 148(2020), no. 7, 3163–3173.CrossRefGoogle Scholar
Lauret, E. A. and Miatello, R. J., Strong representation equivalence for compact symmetric spaces of real rank one . Pacific J. Math. 314(2021), no. 2, 333–373.CrossRefGoogle Scholar
Lauret, E. A., Miatello, R. J., and Rossetti, J. P., Representation equivalence and p-spectrum of constant curvature space forms . J. Geom. Anal. 25(2015), no. 1, 564–591.CrossRefGoogle Scholar
Yozô, M., A formula for the Betti numbers of compact locally symmetric Riemannian manifolds . J. Differential Geometry 1(1967), 99–109.Google Scholar
Yozô, M. and Shingo, M., On certain cohomology groups attached to Hermitian symmetric spaces. II . Osaka Math. J. 5(1968), 223–241.Google Scholar
Milnor, J., Eigenvalues of the Laplace operator on certain manifolds . Proc. Nat. Acad. Sci. U.S.A. 51(1964), 542.CrossRefGoogle ScholarPubMed
Hubert, P., Variétés hyperboliques et elliptiques fortement isospectrales . J. Funct. Anal. 134(1995), no. 2, 363–391.Google Scholar
Rajan, C. S., Some questions on spectrum and arithmetic of locally symmetric spaces . In: Nakamura, I. and Weng, L. (eds.), Algebraic and arithmetic structures of moduli spaces (Sapporo 2007), Advanced Studies in Pure Mathematics, 58, Mathematical Society of Japan, Tokyo, 2010, pp. 137–157.CrossRefGoogle Scholar
Sunada, T., Riemannian coverings and isospectral manifolds . Ann. Math. 121(1985), 169–186.CrossRefGoogle Scholar
Vignéras, M.-F., Variétés Riemanniennes isospectrales et non isométriques . Ann. Math. 112(1980), 21–32.CrossRefGoogle Scholar
Wallach, N. R., On the Selberg trace formula in the case of compact quotient . Bull. Amer. Math. Soc. 82(1976), no. 2, 171–195.CrossRefGoogle Scholar
Williams Floyd, L., Lectures on the spectrum of ${L}^2(\varGamma \,{\backslash}\, G)$ , Pitman Research Notes in Mathematics Series, 242, Longman Scientific and Technical, Harlow; copublished in the United States with John Wiley and Sons, Inc., New York, 1991. xiv+348 pp.Google Scholar