Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T19:28:17.317Z Has data issue: false hasContentIssue false
  • English
  • Français

On Generalized Third Dimension Subgroups

Published online by Cambridge University Press:  20 November 2018

Ken-Ichi Tahara ,
L.R. Vermani  and
Atul Razdan
Ken-Ichi Tahara
Affiliation:
Department of Mathematical Science Aichi University of Education Kariya-shi Japan 448, e-mail: [email protected]
L.R. Vermani
Affiliation:
Department of Mathematics Kurukshetra University Kurukshetra 136 119 (Haryana) India, e-mail: [email protected]
Atul Razdan
Affiliation:
School of Sciences IGNOU, Maidan Garhi New Dehli 110 068 India, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 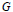$G$ be any group, and 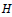$H$ be a normal subgroup of 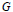$G$. Then M. Hartl identified the subgroup 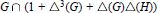$G\,\cap \,(1+\,{{\Delta }^{3}}\,(G)\,+\,\Delta (G)\Delta (H))$ of 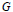$G$. In this note we give an independent proof of the result of Hartl, and we identify two subgroups 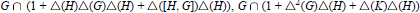$G\,\cap \,(1\,+\,\Delta (H)\Delta (G)\Delta (H)\,+\,\Delta (\left[ H,\,G \right]\Delta (H)),\,G\,\cap \,(1\,+\,{{\Delta }^{2}}\,(G)\Delta (H)\,+\,\Delta (K)\Delta (H))$ of $G$ for some subgroup $K$ of 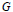$G$ containing 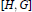$[H,G]$.

Keywords

20C0716S34
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 1 , 01 March 1998 , pp. 109 - 117
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Curzio, M. and Gupta, C. K., Second Fox subgroup of arbitrary groups. Canad. Math. Bull. 38 (1995), 177–181.Google Scholar
2. Hartl, M., On relative polynomial construction of degree 2 and application. (preprint).Google Scholar
3. Khambadkone, M., On the structure of augmentation ideals in group rings. J. Pure Appl. Algebra 35 (1985), 35–45.Google Scholar
4. Karan, R. and Vermani, L. R., A note on polynomial maps, J. Pure Appl. Algebra 51 (1988), 169–173.Google Scholar
5. Karan, R. and Vermani, L. R., Augmentation quotients of integral group rings. J. Indian Math. Soc. 54 (1989), 107–120.Google Scholar
6. Magnus, W., Karass, A. and Solitar, A., Combinatorial Group Theory. 2nd Ed. Dover, 1974.Google Scholar
7. Passi, I. B. S., Polynomial maps on groups-II. Math. Z. 135 (1974), 137–141.Google Scholar
8. Passi, I. B. S. and S. Sharma, The third dimension subgroup mod n. J. London Math. Soc. 9 (1974), 176–182.Google Scholar
9. Sandling, R., The dimension subgroup problem. J. Algebra 21 (1972), 216–231.Google Scholar
10. Vermani, L. R., Razdan, A. and Karan, R., Some remarks on subgroups determined by certain ideals in integral group rings. Proc. Indian Acad. Sci. Math. Sci. 103 (1993), 249–256.Google Scholar