Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T05:18:19.763Z Has data issue: false hasContentIssue false
  • English
  • Français

On Ergodic Extensions of Stationary Measures with Minimal Support

Published online by Cambridge University Press:  20 November 2018

William B. Krebs  and
James B. Robertson
William B. Krebs
Affiliation:
Department of Mathematics, University of CaliforniaSanta Barbara, CA 93106, U.S.A.
James B. Robertson
Affiliation:
Department of Mathematics, University of CaliforniaSanta Barbara, CA 93106, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let T be an ergodic measure preserving transformation with the following property: there exists a positive integer n and a finite partition α such that the number of atom of 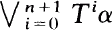is one more than that of 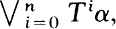, and the probability of at least one of the atoms is irrational. Then there exists a unique (up to conjugacy) transformation S such that there is a partition β with S restricted to 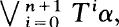isomorphic to T restricted to 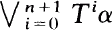and the number of atoms in 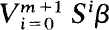is one more than the number of atoms in 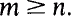for all m ≥ n. Moreover this transformation has discrete spectrum with at most two generators. If there are two generators, one of them must be a root of unity.

Keywords

28D05secondary 60G10
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 26 , Issue 1 , 01 March 1983 , pp. 20 - 25
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Friedman, N. A. (1970), Introduction to Ergodic Theory. Van Nostrand and Reinhold, New York.Google Scholar
2. Halmos, P. (1956), Ergodic Theory, Chelsea, New York.Google Scholar
3. Hlvisaker, N. and Hlvisaker, N. (1965), Some structure theorems for stationary probability measures on finite state sequences. Anns, of Math. Statis. 35, 550-556.Google Scholar