Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T02:15:08.447Z Has data issue: false hasContentIssue false
  • English
  • Français

On Edge-Disjoint Cycles in a Graph

Published online by Cambridge University Press:  20 November 2018

J. W. Moon
J. W. Moon*
Affiliation:
University College London
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

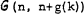Let g(k) denote the least integer such that every graph , with n vertices and n+g(k) edges, contains at least k edge-disjoint cycles; let h(k) be similarly defined for planar graphs. Loops and multiple edges (i.e., cycles of length one and two) are permitted in both cases.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 7 , Issue 4 , December 1964 , pp. 519 - 523
Copyright
Copyright © Canadian Mathematical Society 1964

References

1. Dirac, G. and Erdős, P., On the maximal number of independent circuits in a graph, Acta Math. Acad. Sci. Hung. 14 (1963), 79–94.CrossRefGoogle Scholar
2. Erdős, P.and Pósa, L., On the maximal number of disjoint circuits in a graph, Publ. Math. Debrecen 9 (1962), 3–12.Google Scholar
3. Grűnbaum, B. and Motzkin, T.S., The number of hexagons and the simplicity of geodesies on certain polyhedra, Canad. J. Math. 15 (1963), 744–751.CrossRefGoogle Scholar
4. Steinitz, E., Vorlesungen fiber die Th?orie der Polyeder (Berlin, 1934).Google Scholar